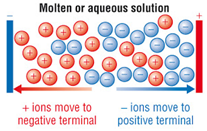
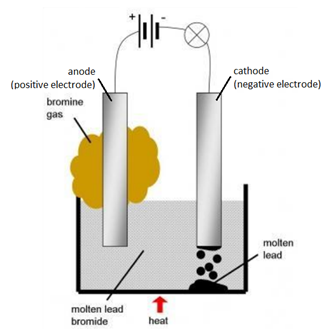
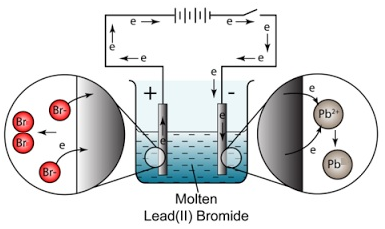
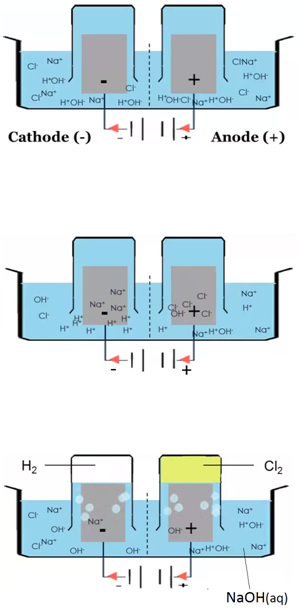
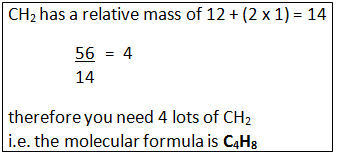Concentration is a measurement of the amount of substance per unit volume.
In Chemistry, concentration is measured in mol/dm3 (read as moles per cubic decimetre).
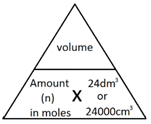
The following formula allows for the interconversion between a concentration (in mol/dm3), the amount (in moles) of a substance in a solution, and the volume of the solution (in dm3).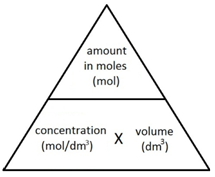
![Rendered by QuickLaTeX.com \[amount(mol) = concentration(mol/dm^3) \times volume(dm^3) \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27447%27%20height%3D%2722%27%20viewBox%3D%270%200%20447%2022%27%3E%3Crect%20width%3D%27447%27%20height%3D%2722%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
or
![Rendered by QuickLaTeX.com \[concentration(mol/dm^3) = \frac{amount(mol)}{volume(dm^3)} \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27325%27%20height%3D%2742%27%20viewBox%3D%270%200%20325%2042%27%3E%3Crect%20width%3D%27325%27%20height%3D%2742%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
Note: 1 dm3 = 1000 cm3
For example, to convert 250 cm3 into dm3:
![Rendered by QuickLaTeX.com \[250cm^3 = \frac{250}{1000} \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27119%27%20height%3D%2738%27%20viewBox%3D%270%200%20119%2038%27%3E%3Crect%20width%3D%27119%27%20height%3D%2738%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
![Rendered by QuickLaTeX.com \[250cm^3 = 0.25dm^3 \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27145%27%20height%3D%2717%27%20viewBox%3D%270%200%20145%2017%27%3E%3Crect%20width%3D%27145%27%20height%3D%2717%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
Example 1: 0.03 mol of sodium carbonate (Na2CO3) is dissolved in 300 cm3 of water. Calculate the concentration of the solution.
Step 1: Convert the volume of water from cm3 into dm3.
![Rendered by QuickLaTeX.com \[volume = 300cm^3 \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27138%27%20height%3D%2717%27%20viewBox%3D%270%200%20138%2017%27%3E%3Crect%20width%3D%27138%27%20height%3D%2717%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
![Rendered by QuickLaTeX.com \[volume = \frac{300}{1000}dm^3 \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27153%27%20height%3D%2737%27%20viewBox%3D%270%200%20153%2037%27%3E%3Crect%20width%3D%27153%27%20height%3D%2737%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
![Rendered by QuickLaTeX.com \[volume = 0.300dm^3 \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27154%27%20height%3D%2717%27%20viewBox%3D%270%200%20154%2017%27%3E%3Crect%20width%3D%27154%27%20height%3D%2717%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
Step 2: Use the molar concentration formula to calculate of the concentration of the solution.
![Rendered by QuickLaTeX.com \[concentration = \frac{amount}{volume} \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27196%27%20height%3D%2736%27%20viewBox%3D%270%200%20196%2036%27%3E%3Crect%20width%3D%27196%27%20height%3D%2736%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
![Rendered by QuickLaTeX.com \[concentration = \frac{0.03}{0.300} \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27176%27%20height%3D%2736%27%20viewBox%3D%270%200%20176%2036%27%3E%3Crect%20width%3D%27176%27%20height%3D%2736%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
![Rendered by QuickLaTeX.com \[concentration = 0.1 mol/dm^3 \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27227%27%20height%3D%2722%27%20viewBox%3D%270%200%20227%2022%27%3E%3Crect%20width%3D%27227%27%20height%3D%2722%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
Example 2: Calculate the amount, in moles, of 25cm3 of hydrochloric acid (HCl) with a concentration of 2 mol/dm3.
Step 1: Convert the volume of HCl from cm3 into dm3.
![Rendered by QuickLaTeX.com \[volume = 25cm^3 \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27130%27%20height%3D%2717%27%20viewBox%3D%270%200%20130%2017%27%3E%3Crect%20width%3D%27130%27%20height%3D%2717%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
![Rendered by QuickLaTeX.com \[volume = \frac{25}{1000}dm^3 \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27153%27%20height%3D%2738%27%20viewBox%3D%270%200%20153%2038%27%3E%3Crect%20width%3D%27153%27%20height%3D%2738%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
![Rendered by QuickLaTeX.com \[volume = 0.025dm^3 \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27154%27%20height%3D%2717%27%20viewBox%3D%270%200%20154%2017%27%3E%3Crect%20width%3D%27154%27%20height%3D%2717%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
Step 2: Rearrange the molar concentration formula to calculate of the amount, in moles of HCl.
![Rendered by QuickLaTeX.com \[amount= concentration \times volume \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27273%27%20height%3D%2713%27%20viewBox%3D%270%200%20273%2013%27%3E%3Crect%20width%3D%27273%27%20height%3D%2713%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
![Rendered by QuickLaTeX.com \[amount = 2 \times 0.025 \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27155%27%20height%3D%2713%27%20viewBox%3D%270%200%20155%2013%27%3E%3Crect%20width%3D%27155%27%20height%3D%2713%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
![Rendered by QuickLaTeX.com \[amount = 0.050 mol \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27154%27%20height%3D%2713%27%20viewBox%3D%270%200%20154%2013%27%3E%3Crect%20width%3D%27154%27%20height%3D%2713%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
Titration calculations, example 1
The titration method that is used to prepare a soluble salt is also used to determine the concentration of an unknown solution.
For example, a titration problem will look like this:
A pupil carried out a titration to find the concentration of a solution of hydrochloric acid (HCl). She found that 25.0 cm3 of 0.100 mol/dm3 sodium hydroxide solution (NaOH) required 23.50 cm3 of dilute hydrochloric acid for neutralisation. Calculate the concentration, in mol/dm3 of the acid.
The chemical equation for this reaction is:
NaOH(aq) + HCl(aq) –> NaCl(aq) + H2O(l)
volume 25.0cm3 23.50cm3
concentration 0.100mol/dm3
It can be useful, as shown above, to write the values of the volumes & concentration underneath the equation.
Step 1: Calculate the amount, in moles, of the solution that you know the values for both volume and concentration. In this case sodium hydroxide (NaOH).
First convert the volume of NaOH from cm3 into dm3.
![Rendered by QuickLaTeX.com \[volume = 25cm^3 \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27130%27%20height%3D%2717%27%20viewBox%3D%270%200%20130%2017%27%3E%3Crect%20width%3D%27130%27%20height%3D%2717%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
![Rendered by QuickLaTeX.com \[volume = \frac{25}{1000}dm^3 \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27153%27%20height%3D%2738%27%20viewBox%3D%270%200%20153%2038%27%3E%3Crect%20width%3D%27153%27%20height%3D%2738%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
![Rendered by QuickLaTeX.com \[volume = 0.025dm^3 \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27154%27%20height%3D%2717%27%20viewBox%3D%270%200%20154%2017%27%3E%3Crect%20width%3D%27154%27%20height%3D%2717%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
Then rearrange the molar concentration formula to calculate of the amount, in moles of NaOH.
![Rendered by QuickLaTeX.com \[amount= concentration \times volume \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27273%27%20height%3D%2713%27%20viewBox%3D%270%200%20273%2013%27%3E%3Crect%20width%3D%27273%27%20height%3D%2713%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
![Rendered by QuickLaTeX.com \[amount = 0.100 \times 0.025 \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27187%27%20height%3D%2714%27%20viewBox%3D%270%200%20187%2014%27%3E%3Crect%20width%3D%27187%27%20height%3D%2714%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
![Rendered by QuickLaTeX.com \[amount = 0.0025 mol \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27164%27%20height%3D%2713%27%20viewBox%3D%270%200%20164%2013%27%3E%3Crect%20width%3D%27164%27%20height%3D%2713%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
Step 2: Deduce the amount, in moles of the solution with the unknown concentration. In this case hydrochloric acid (HCl).
From the chemical equation the ratio of NaOH to HCl is 1:1
Therefore if you have 0.0025 mol of NaOH, this will react with 0.0025 mol of HCl.
Step 3: Calculate the concentration of the hydrochloric acid (HCl).
Convert the volume of HCl from cm3 into dm3.
![Rendered by QuickLaTeX.com \[volume = 23.5cm^3 \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27144%27%20height%3D%2717%27%20viewBox%3D%270%200%20144%2017%27%3E%3Crect%20width%3D%27144%27%20height%3D%2717%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
![Rendered by QuickLaTeX.com \[volume = \frac{23.5}{1000}dm^3 \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27153%27%20height%3D%2738%27%20viewBox%3D%270%200%20153%2038%27%3E%3Crect%20width%3D%27153%27%20height%3D%2738%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
![Rendered by QuickLaTeX.com \[volume = 0.0235dm^3 \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27164%27%20height%3D%2717%27%20viewBox%3D%270%200%20164%2017%27%3E%3Crect%20width%3D%27164%27%20height%3D%2717%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
Use the molar concentration formula to calculate of the concentration of the HCl.
![Rendered by QuickLaTeX.com \[concentration = \frac{amount}{volume} \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27196%27%20height%3D%2736%27%20viewBox%3D%270%200%20196%2036%27%3E%3Crect%20width%3D%27196%27%20height%3D%2736%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
![Rendered by QuickLaTeX.com \[concentration = \frac{0.0025}{0.0235} \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27185%27%20height%3D%2737%27%20viewBox%3D%270%200%20185%2037%27%3E%3Crect%20width%3D%27185%27%20height%3D%2737%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
![Rendered by QuickLaTeX.com \[concentration = 0.106 mol/dm^3 \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27244%27%20height%3D%2722%27%20viewBox%3D%270%200%20244%2022%27%3E%3Crect%20width%3D%27244%27%20height%3D%2722%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
Titration calculations, example 2
25.0 cm3 of sodium carbonate solution (Na2CO3) of unknown concentration was neutralised by 30.0 cm3 of 0.100 mol/dm3 nitric acid (HNO3).
Na2CO3(aq) + 2HNO3(aq) –> 2NaNO3(aq) + CO2(g) + H2O(l)
Calculate the concentration, in mol/dm3 of the sodium carbonate solution.
Step 1: Calculate the amount, in moles, of nitric acid (HNO3).
![Rendered by QuickLaTeX.com \[volume = 30cm^3 \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27130%27%20height%3D%2717%27%20viewBox%3D%270%200%20130%2017%27%3E%3Crect%20width%3D%27130%27%20height%3D%2717%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
![Rendered by QuickLaTeX.com \[volume = \frac{30}{1000}dm^3 \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27153%27%20height%3D%2737%27%20viewBox%3D%270%200%20153%2037%27%3E%3Crect%20width%3D%27153%27%20height%3D%2737%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
![Rendered by QuickLaTeX.com \[volume = 0.030dm^3 \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27154%27%20height%3D%2717%27%20viewBox%3D%270%200%20154%2017%27%3E%3Crect%20width%3D%27154%27%20height%3D%2717%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
![Rendered by QuickLaTeX.com \[amount= concentration \times volume \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27273%27%20height%3D%2713%27%20viewBox%3D%270%200%20273%2013%27%3E%3Crect%20width%3D%27273%27%20height%3D%2713%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
![Rendered by QuickLaTeX.com \[amount = 0.100 \times 0.030 \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27188%27%20height%3D%2713%27%20viewBox%3D%270%200%20188%2013%27%3E%3Crect%20width%3D%27188%27%20height%3D%2713%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
![Rendered by QuickLaTeX.com \[amount = 0.0030 mol \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27164%27%20height%3D%2713%27%20viewBox%3D%270%200%20164%2013%27%3E%3Crect%20width%3D%27164%27%20height%3D%2713%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
Step 2: Deduce the amount, in moles of sodium carbonate (Na2CO3).
Using the equation:
Na2CO3(aq) + 2HNO3(aq) –> 2NaNO3(aq) + CO2(g) + H2O(l)
Ratio Na2CO3:HNO3 = 1:2
![Rendered by QuickLaTeX.com \[amount=\frac{0.0030}{2} = 0.0015mol\]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27240%27%20height%3D%2736%27%20viewBox%3D%270%200%20240%2036%27%3E%3Crect%20width%3D%27240%27%20height%3D%2736%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
Step 3: Calculate the concentration of sodium carbonate (Na2CO3).
![Rendered by QuickLaTeX.com \[volume = 25cm^3 \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27130%27%20height%3D%2717%27%20viewBox%3D%270%200%20130%2017%27%3E%3Crect%20width%3D%27130%27%20height%3D%2717%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
![Rendered by QuickLaTeX.com \[volume = \frac{25}{1000}dm^3 \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27153%27%20height%3D%2738%27%20viewBox%3D%270%200%20153%2038%27%3E%3Crect%20width%3D%27153%27%20height%3D%2738%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
![Rendered by QuickLaTeX.com \[volume = 0.025dm^3 \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27154%27%20height%3D%2717%27%20viewBox%3D%270%200%20154%2017%27%3E%3Crect%20width%3D%27154%27%20height%3D%2717%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
![Rendered by QuickLaTeX.com \[concentration = \frac{amount}{volume} \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27196%27%20height%3D%2736%27%20viewBox%3D%270%200%20196%2036%27%3E%3Crect%20width%3D%27196%27%20height%3D%2736%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
![Rendered by QuickLaTeX.com \[concentration = \frac{0.0015}{0.025} \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27185%27%20height%3D%2737%27%20viewBox%3D%270%200%20185%2037%27%3E%3Crect%20width%3D%27185%27%20height%3D%2737%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
![Rendered by QuickLaTeX.com \[concentration = 0.06 mol/dm^3 \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27235%27%20height%3D%2722%27%20viewBox%3D%270%200%20235%2022%27%3E%3Crect%20width%3D%27235%27%20height%3D%2722%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
Converting mol/dm3 into g/dm3
Concentration can also be expressed in g/dm3 (grams per cubic decimetre).
Therefore mol/dm3 can be converted into g/dm3.
Example: Convert 0.06 mol/dm3 of sodium carbonate (Na2CO3) into g/dm3
Step 1: calculate the relative formula mass (Mr) of sodium carbonate (Na2CO3).
![Rendered by QuickLaTeX.com \[M_r= (2 \times 23) + (1 \times 12) (3 \times 16) = 106 \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27306%27%20height%3D%2718%27%20viewBox%3D%270%200%20306%2018%27%3E%3Crect%20width%3D%27306%27%20height%3D%2718%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
Step 2: Recall the formula giving the relationship between mass, amount and formula mass.
![Rendered by QuickLaTeX.com \[mass= amount(in\,moles) \times M_r \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27250%27%20height%3D%2718%27%20viewBox%3D%270%200%20250%2018%27%3E%3Crect%20width%3D%27250%27%20height%3D%2718%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
therefore
![Rendered by QuickLaTeX.com \[mass/dm^3= moles/dm^3 \times M_r \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27238%27%20height%3D%2722%27%20viewBox%3D%270%200%20238%2022%27%3E%3Crect%20width%3D%27238%27%20height%3D%2722%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
![Rendered by QuickLaTeX.com \[mass/dm^3= 0.06 \times 106\]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27186%27%20height%3D%2722%27%20viewBox%3D%270%200%20186%2022%27%3E%3Crect%20width%3D%27186%27%20height%3D%2722%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
![Rendered by QuickLaTeX.com \[mass/dm^3= 6.36 g/dm^3 \]](data:image/svg+xml,%3Csvg%20xmlns%3D%27http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%27%20width%3D%27188%27%20height%3D%2722%27%20viewBox%3D%270%200%20188%2022%27%3E%3Crect%20width%3D%27188%27%20height%3D%2722%27%20fill-opacity%3D%220%22%2F%3E%3C%2Fsvg%3E)
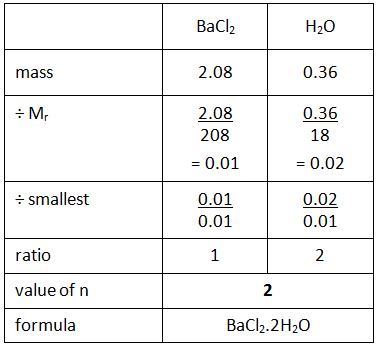
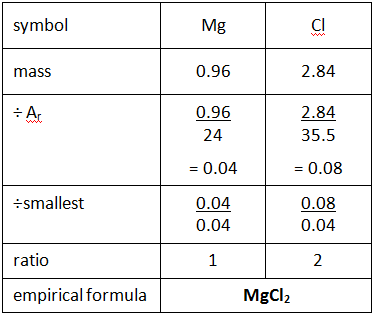 Example: What is the empirical formula of magnesium chloride if 0.96 g of magnesium combines with 2.84 g of chlorine?
Example: What is the empirical formula of magnesium chloride if 0.96 g of magnesium combines with 2.84 g of chlorine?