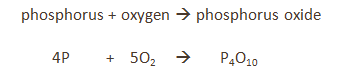1:24 understand why the noble gases (Group 0) do not readily react
The noble gases are inert (unreactive) because they have a full outer shell of electrons.
The noble gases are inert (unreactive) because they have a full outer shell of electrons.
Example:
Sodium (Na) reacts with water (H2O) to produce a solution of sodium hydroxide (NaOH) and hydrogen gas (H2).
Word equation:
sodium + water –> sodium hydroxide + hydrogen
Writing the chemical equation
A chemical equation represents what happens in terms of atoms in a chemical reaction.
Step 1: To write a chemical equation we need to know the chemical formulae of the substances.
Na + H2O –> NaOH + H2
Step 2: The next step is to balance the equation: write a large number before each compound so the number of atoms of each element on the left hand side (reactants) matches the number on the right (products). This large number is the amount of each compound or element.
During this balancing stage the actual formulas for each compound must not be changed. Only the number of each compound changes.
2Na + 2H2O –> 2NaOH + H2
If asked for an equation, the chemical equation must be given.
State symbols are used to show what physical state the reactants and products are in.
| State symbols | Physical state |
|---|---|
| (s) | Solid |
| (l) | Liquid |
| (g) | Gas |
| (aq) | Aqueous solution (dissolved in water) |
Example:
A solid piece of sodium (Na) reacts with water (H2O) to produce a solution of sodium hydroxide (NaOH) and hydrogen gas (H2).
2Na(s) + 2H2O(l) –> 2NaOH(aq) + H2(g)
Relative formula mass (Mr) is mass of a molecule or compound (on a scale compared to carbon-12).
It is calculated by adding up the relative atomic masses (Ar) of all the atoms present in the formula.
Example:
The relative formula mass (Mr) for water (H2O) is 18.
Water = H2O
Atoms present = (2 x H) + (1 x O)
Mr = (2 x 1) + (1 x 16) = 18
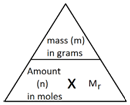
In Chemistry, the mole is a measure of amount of substance (n).
The abbreviation for mole is mol.
The mass of 1 mole of a substance is the relative formula mass (Mr) of the substance in grams.
Example:
The Mr of water is 18.
Therefore the mass of 1 mol of water equals 18 g.
The following formula allows for the interconversion between a mass in grams and a number of moles for a given substance:
Example 1:
Calculate the amount, in moles, of 8.8 g of carbon dioxide (CO2).
Step 1: Calculate the relative formula mass (Mr) of carbon dioxide (CO2).
Step 2: Use the formula to calculate the amount in moles.
Example 2:
Calculate the mass of 2 mol of copper(II) sulfate (CuSO4).
Step 1: Calculate the relative formula mass (Mr) of copper(II) sulfate (CuSO4).
Step 2: Rearrange the formula to calculate the mass.
Example: When calcium carbonate (CaCO3) is heated calcium oxide is produced. You can use reacting mass calculations to calculate the mass of calcium oxide produced when heating 25 g of calcium carbonate.
CaCO3 –> CaO + CO2
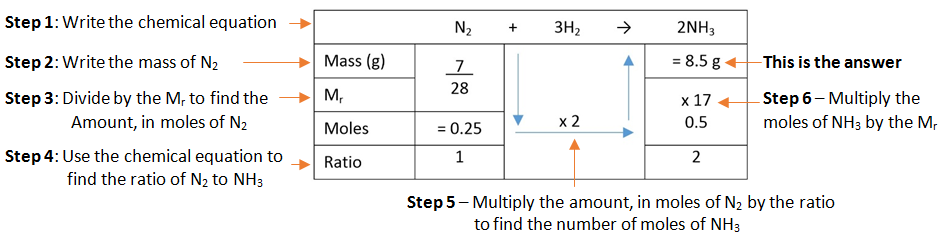
Step 1: Calculate the amount, in moles, of 25 g of calcium carbonate (CaCO3)
Step 2: Deduce the amount, in moles, of CaO produced from 0.25 mol of CaCO3.
This step involves using the ratio of CaCO3 to CaO from the chemical equation.
CaCO3 –> CaO + CO2
From the equation you can see that the ratio of CaCO3 to CaO is 1:1.
Therefore if you have 0.25 mol of CaCO3 this will produced 0.25 mol of CaO.
Step 3: Calculate the mass of 0.25 mol of CaO.
A simple format for laying out this method can be used.
Example: What mass of ammonia (NH3) is formed when 7 g of nitrogen (N2) is combined with hydrogen (H2).
Yield is how much product you get from a chemical reaction.
The theoretical yield is the amount of product that you would expect to get. This is calculated using reacting mass calculations.
In most chemical reactions, however, you rarely achieved your theoretical yield.
For example, in the following reaction:
CaCO3 –> CaO + CO2
You might expect to achieve a theoretical yield of 56 g of CaO from 100 g of CaCO3.
However, what if the actual yield is only 48 g of CaO.
By using the following formula, the % yield can be calculated:
Finding the formula of a metal oxide experimentally
The formulae of metal oxides can be found experimentally by reacting a metal with oxygen and recording the mass changes.
Example: When magnesium is burned in air, it reacts with oxygen (O2) to form magnesium oxide (MgO).
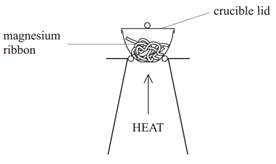
Method:
• Weigh a crucible and lid
• Place the magnesium ribbon in the crucible, replace the lid, and reweigh
• Calculate the mass of magnesium
(mass of crucible + lid + Magnesium – mass of crucible + lid)
• Heat the crucible with lid on until the magnesium burns
(lid prevents magnesium oxide escaping therefore ensuring accurate results)
• Lift the lid from time to time (this allows air to enter)
• Stop heating when there is no sign of further reaction
(this ensures all Mg has reacted)
• Allow to cool and reweigh
• Repeat the heating , cooling and reweigh until two consecutive masses are the same
(this ensures all Mg has reacted and therefore the results will be accurate)
• Calculate the mass of magnesium oxide formed (mass of crucible + lid + Magnesium oxide – mass of crucible + lid)
Finding the formula of a metal oxide experimentally
The formulae of metal oxides can be found experimentally by reacting a metal with oxygen and recording the mass changes.
Example: When magnesium is burned in air, it reacts with oxygen (O2) to form magnesium oxide (MgO).

Method:
• Weigh a crucible and lid
• Place the magnesium ribbon in the crucible, replace the lid, and reweigh
• Calculate the mass of magnesium
(mass of crucible + lid + Magnesium – mass of crucible + lid)
• Heat the crucible with lid on until the magnesium burns
(lid prevents magnesium oxide escaping therefore ensuring accurate results)
• Lift the lid from time to time (this allows air to enter)
• Stop heating when there is no sign of further reaction
(this ensures all Mg has reacted)
• Allow to cool and reweigh
• Repeat the heating , cooling and reweigh until two consecutive masses are the same
(this ensures all Mg has reacted and therefore the results will be accurate)
• Calculate the mass of magnesium oxide formed (mass of crucible + lid + Magnesium oxide – mass of crucible + lid)
Finding the formula of a salt containing water of crystallisation
When some substances crystallise from solution, water becomes chemically bound up with the salt. This is called water of crystallisation and the salt is said to be hydrated. For example, hydrated copper sulfate has the formula CuSO4.5H2O which formula indicates that for every CuSO4 in a crystal there are five water (H2O) molecules.
When you heat a salt that contains water of crystallisation, the water is driven off leaving the anhydrous (without water) salt behind. If the hydrated copper sulfate (CuSO4.5H2O) are strongly heated in a crucible then they will break down and the water lost, leaving behind anhydrous copper sulfate (CuSO4). The method followed is similar to that for metal oxides, as shown above. The difference of mass before and after heating is the mass of the water lost. These mass numbers can be used to obtain the formula of the salt.
The empirical formula shows the simplest whole-number ratio between atoms/ions in a compound.
The molecular formula shows the actual number of atoms of each type of element in a molecule.
For example, for ethane:
Molecular formula = C2H6
Empirical formula = CH3
Here are some more examples:
| Name | Molecular formula | Empirical Formula |
|---|---|---|
| pentene | C5H10 | CH2 |
| butene | C4H8 | CH2 |
| glucose | C6H12O6 | CH2O |
| hydrogen peroxide | H2O2 | HO |
| propane | C3H8 | C3H8 |
Notice from the table that several different molecules can have the same empirical formula, which means that it is not possible to deduce the molecular formula from the empirical formula without some additional information. Also notice that sometimes it is not possible to simplify a molecular formula into simpler whole-number ratio, in which case the empirical formula is equal to the molecular formula.
Calculating the Empirical Formula
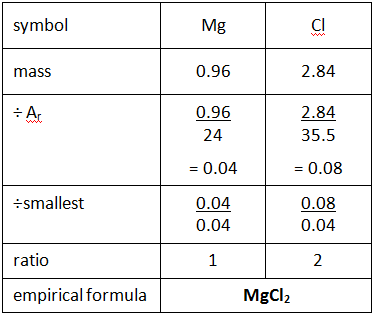 Example: What is the empirical formula of magnesium chloride if 0.96 g of magnesium combines with 2.84 g of chlorine?
Example: What is the empirical formula of magnesium chloride if 0.96 g of magnesium combines with 2.84 g of chlorine?
Step 1: Put the symbols for each element involved at the top of the page.
Step 2: Underneath, write down the masses of each element combining.
Step 3: Divide by their relative atomic mass (Ar).
Step 4: Divide all the numbers by the smallest of these numbers to give a whole number ratio.
Step 5: Use this to give the empirical formula.
(If your ratio is 1:1.5 then multiple each number by 2
If your ratio is 1:1.33 then x3. If your ratio is 1:1.25 x4)
Calculating the Molecular Formula
If you know the empirical formula and the relative formula mass you can work out the molecular formula of a compound.
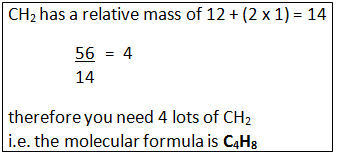
Example: A compound has the empirical formula CH2, and its relative formula mass is 56. Calculate the molecular formula.
Step 1: Calculate the relative mass of the empirical formula.
Step 2: Find out the number of times the relative mass of the empirical formula goes into the Mr of the compound.
Step 3: This tells how many times bigger the molecule formula is compared to the empirical formula.
Empirical formula calculations involving water of crystallisation
When you heat a salt that contains water of crystallisation, the water is driven off leaving the anhydrous (without water) salt behind. For example, barium chloride crystals contain water of crystallisation, and therefore would have the formula BaCl2.nH2O where the symbol ‘n’ indicates the number of molecules of water of crystallisation. This value can be calculated using the following method.
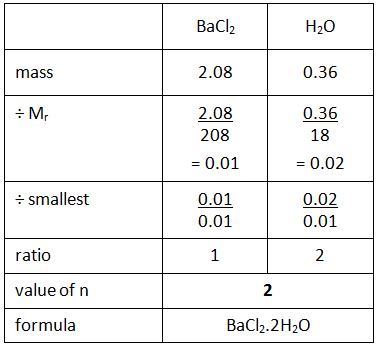
Example: If you heated hydrated barium chloride (BaCl2.nH2O) in a crucible you might end up with the following results.

Step 1: Calculate the mass of the anhydrous barium chloride (BaCl2) and the water (H2O) driven off.

Step 2: Use the empirical formula method to find the value of n in the formula.
Concentration is a measurement of the amount of substance per unit volume.
In Chemistry, concentration is measured in mol/dm3 (read as moles per cubic decimetre).
The following formula allows for the interconversion between a concentration (in mol/dm3), the amount (in moles) of a substance in a solution, and the volume of the solution (in dm3).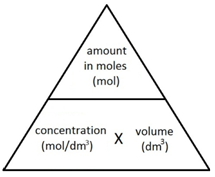
or
Note: 1 dm3 = 1000 cm3
For example, to convert 250 cm3 into dm3:
Example 1: 0.03 mol of sodium carbonate (Na2CO3) is dissolved in 300 cm3 of water. Calculate the concentration of the solution.
Step 1: Convert the volume of water from cm3 into dm3.
Step 2: Use the molar concentration formula to calculate of the concentration of the solution.
Example 2: Calculate the amount, in moles, of 25cm3 of hydrochloric acid (HCl) with a concentration of 2 mol/dm3.
Step 1: Convert the volume of HCl from cm3 into dm3.
Step 2: Rearrange the molar concentration formula to calculate of the amount, in moles of HCl.
Titration calculations, example 1
The titration method that is used to prepare a soluble salt is also used to determine the concentration of an unknown solution.
For example, a titration problem will look like this:
A pupil carried out a titration to find the concentration of a solution of hydrochloric acid (HCl). She found that 25.0 cm3 of 0.100 mol/dm3 sodium hydroxide solution (NaOH) required 23.50 cm3 of dilute hydrochloric acid for neutralisation. Calculate the concentration, in mol/dm3 of the acid.
The chemical equation for this reaction is:
NaOH(aq) + HCl(aq) –> NaCl(aq) + H2O(l)
volume 25.0cm3 23.50cm3
concentration 0.100mol/dm3
It can be useful, as shown above, to write the values of the volumes & concentration underneath the equation.
Step 1: Calculate the amount, in moles, of the solution that you know the values for both volume and concentration. In this case sodium hydroxide (NaOH).
First convert the volume of NaOH from cm3 into dm3.
Then rearrange the molar concentration formula to calculate of the amount, in moles of NaOH.
Step 2: Deduce the amount, in moles of the solution with the unknown concentration. In this case hydrochloric acid (HCl).
From the chemical equation the ratio of NaOH to HCl is 1:1
Therefore if you have 0.0025 mol of NaOH, this will react with 0.0025 mol of HCl.
Step 3: Calculate the concentration of the hydrochloric acid (HCl).
Convert the volume of HCl from cm3 into dm3.
Use the molar concentration formula to calculate of the concentration of the HCl.
Titration calculations, example 2
25.0 cm3 of sodium carbonate solution (Na2CO3) of unknown concentration was neutralised by 30.0 cm3 of 0.100 mol/dm3 nitric acid (HNO3).
Na2CO3(aq) + 2HNO3(aq) –> 2NaNO3(aq) + CO2(g) + H2O(l)
Calculate the concentration, in mol/dm3 of the sodium carbonate solution.
Step 1: Calculate the amount, in moles, of nitric acid (HNO3).
Step 2: Deduce the amount, in moles of sodium carbonate (Na2CO3).
Using the equation:
Na2CO3(aq) + 2HNO3(aq) –> 2NaNO3(aq) + CO2(g) + H2O(l)
Ratio Na2CO3:HNO3 = 1:2
Step 3: Calculate the concentration of sodium carbonate (Na2CO3).
Converting mol/dm3 into g/dm3
Concentration can also be expressed in g/dm3 (grams per cubic decimetre).
Therefore mol/dm3 can be converted into g/dm3.
Example: Convert 0.06 mol/dm3 of sodium carbonate (Na2CO3) into g/dm3
Step 1: calculate the relative formula mass (Mr) of sodium carbonate (Na2CO3).
Step 2: Recall the formula giving the relationship between mass, amount and formula mass.
therefore
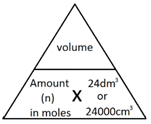
The molar volume of a gas is the volume that one mole of any gas will occupy.
1 mole of gas, at room temperature and pressure (rtp), will always occupy 24 dm3 or 24,000 cm3.
Note: 1 dm3 = 1000 cm3
The following formulae allows for the interconversion between a volume in dm3 or cm3 and a number of moles for a given gas:
or
Example 1:
Calculate the amount, in moles, of 12 dm3 of carbon dioxide (CO2).
Example 2:
Calculate the volume at rtp in cubic centimetres (cm3), of 3 mol of oxygen, (O2).
To determine the formula of a metal oxide by combustion.
Example: When magnesium is burned in air, it reacts with oxygen (O2) to form magnesium oxide (MgO).
2Mg + O2 –> 2MgO

Method:
It is then possible to use this data to calculate the empirical formula of the metal oxide.
To determine the formula of a metal oxide by reduction
Example: When copper (II) oxide is heated in a stream of methane, the oxygen is removed from the copper (II) oxide, producing copper, carbon dioxide and water:
4CuO + CH4 –> 4Cu + CO2 + 2H2O
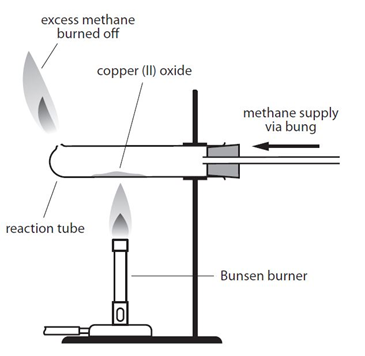
By comparing the mass of copper produced with the mass of copper oxide used it is possible to determine the formula of the copper oxide.
As an alternative, hydrogen gas could be used instead of methane:
CuO + H2 –> Cu + H2O
It is then possible to use this data to calculate the empirical formula of the metal oxide.
There is an important safety point to note with both versions of this experiment. Both methane and hydrogen are explosive if ignited with oxygen. It is important that a good supply of the the gas is allowed to fill the tube before the gas it lit. This flushes out any oxygen from the tube, so the gas will only burn when it exits the tube and comes into contact with oxygen in the air.
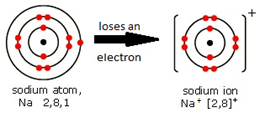
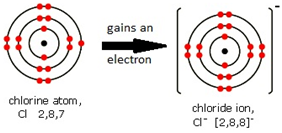
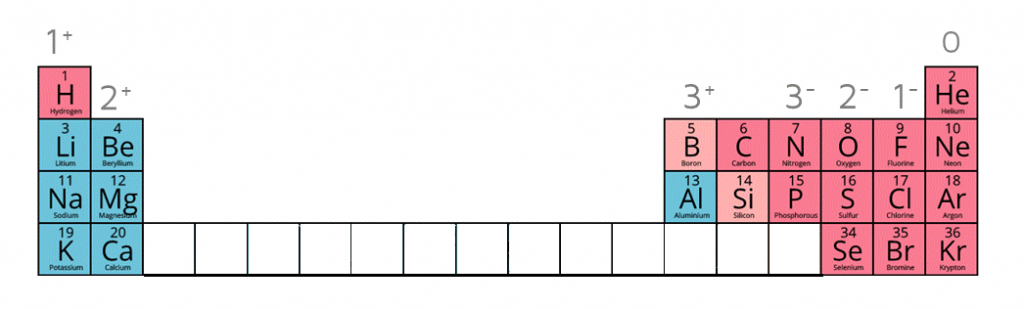
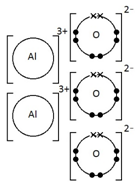
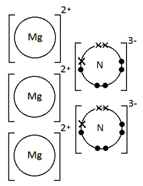
Ions are electrically charged particles formed when atoms lose or gain electrons.
They have the same electronic structures as noble gases.
Metal atoms form positive ions (cations).
Non-metal atoms form negative ions (anions).
When given this information of the following ions, it is possible to work out the formulae of ionic compounds which include these ions.
| Name of Ion | Formula | Charge |
|---|---|---|
| Sulfate | SO42- | -2 |
| Carbonate | CO32- | -2 |
| Nitrate | NO3- | -1 |
| Hydroxide | OH- | -1 |
| Ammonium | NH4+ | +1 |
| Silver ion | Ag+ | +1 |
| Zinc ion | Zn2+ | +2 |
| Hydrogen ion | H+ | +1 |
| Copper (II) ion | Cu2+ | +2 |
| Iron (II) ion | Fe2+ | +2 |
| Iron (III) ion | Fe3+ | +3 |
| Lead (II) ion | Pb2+ | +2 |
Ion charges on the periodic table
| Name of Ion | Formula | Charge |
|---|---|---|
| Sulfate | SO42- | -2 |
| Carbonate | CO32- | -2 |
| Nitrate | NO3- | -1 |
| Hydroxide | OH- | -1 |
| Ammonium | NH4+ | +1 |
| Hydrogen ion | H+ | +1 |
Ion charges on the periodic table

| Name of Ion | Formula | Charge |
|---|---|---|
| Sulfate | SO42- | -2 |
| Carbonate | CO32- | -2 |
| Nitrate | NO3- | -1 |
| Hydroxide | OH- | -1 |
| Ammonium | NH4+ | +1 |
| Silver ion | Ag+ | +1 |
| Zinc ion | Zn2+ | +2 |
| Hydrogen ion | H+ | +1 |
| Copper (II) ion | Cu2+ | +2 |
| Iron (II) ion | Fe2+ | +2 |
| Iron (III) ion | Fe3+ | +3 |
| Lead (II) ion | Pb2+ | +2 |
Ion charges on the periodic table

Writing the electron configuration of an atom allows you to work out the electron configuration of the ion and therefore the charge on the ion.
Examples:
Atom = Mg
Electron configuration = 2,8,2
remove the two electrons from the outer shell to achieve the same electron configuration as the nearest noble gas, Neon (Ne 2,8)
Ion = Mg2+
Atom = O
Electron configuration = 2,6
add two electrons to the outer shell to achieve the same electron configuration as the nearest noble gas, Neon (Ne 2,8)
Ion = O2- [2,8]2-
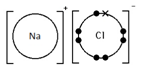
Sodium chloride, NaCl
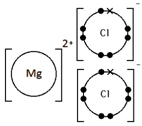
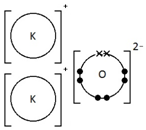
Calcium oxide, CaO
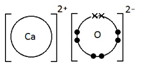
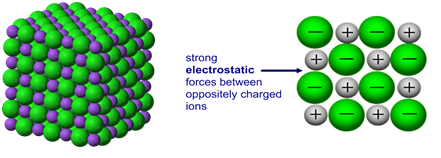
Ionic bonding: a strong electrostatic attraction between oppositely charged ions.
Ionic compounds have high melting and boiling points because they have a giant structure with strong electrostatic forces between oppositely charged ions that require a lot of energy to break.
Giant 3D lattice of sodium chloride (NaCl)
Ionic compounds do not conduct electricity when solid.
However, ionic compounds do conduct electricity if molten or in solution.
A covalent bond is formed between two non-metal atoms by sharing a pair of electrons in order to fill the outer shell.
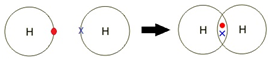
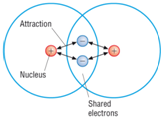
Covalent bonding: a strong attraction between a shared pair of electrons and two nuclei.
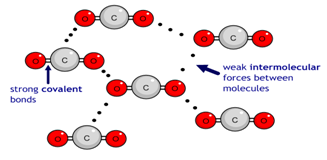
Carbon dioxide (CO2) has a simple molecular structure. This just means that it is made up of molecules.
Within each molecule are atoms bonded to each other covalently. These covalent bonds inside the molecules are strong.
However, between the molecules are weak forces of attraction that require little energy to break. These forces are not covalent bonds. This is why simple molecular substances such as carbon dioxide have a low boiling point.
So when carbon dioxide changes from a solid to a gas, for example, that process can be represented as:
CO₂ (s) → CO₂ (g)
Notice that even though there has been a dramatic change of state from solid to gas, the substance before and after the change is always made up of carbon dioxide molecules. During the change of the state the covalent bonds within each molecule remain unbroken. Instead it is the weak forces of attraction between the molecules which have been overcome.
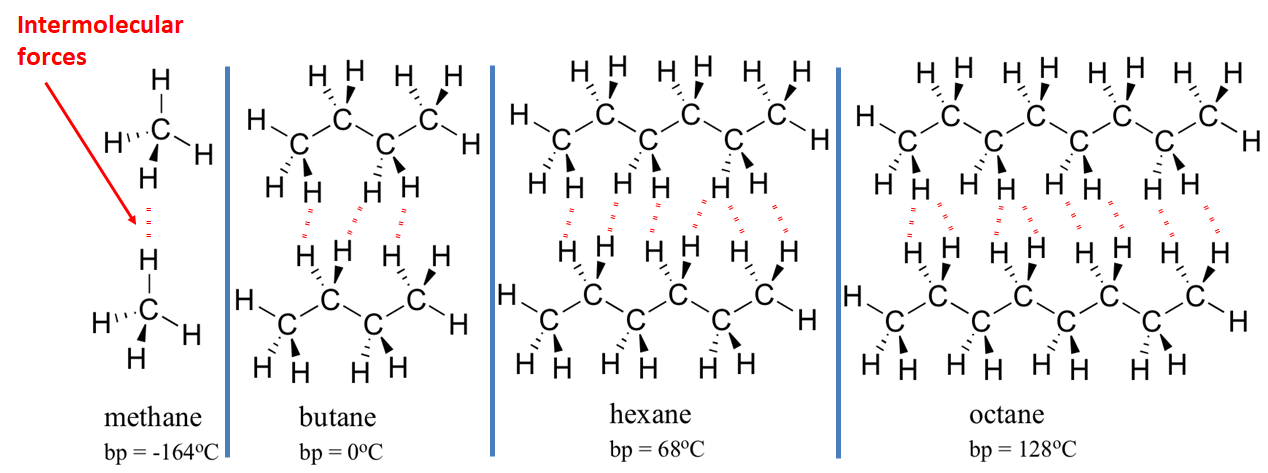
Larger molecules tend to have higher boiling points.
This is because larger molecules (molecules with more mass) have more forces of attraction between them. These forces, although weak, must be overcome if the substance is to boil, and larger molecules have more attractions which must be overcome.
Diamond has a high melting point because it is a giant covalent structure with many strong covalent bonds that require a lot of energy to break.
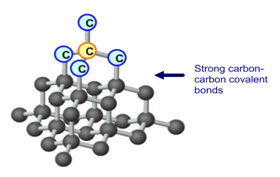
Allotropes are different forms of the same element. Three different allotropes of carbon are shown here as examples: diamond, graphite and C60 fullerene.
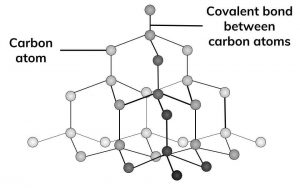
Diamond is made up of only carbon atoms, in a giant 3D lattice, where each of those atoms has a strong covalent bonds to 4 other carbon. Every one of carbon’s 4 outer electrons is involved in one of these strong covalent bonds.
Diamond is extremely hard because it is a giant covalent structure with many strong covalent bonds.
Because it is hard, diamond is used in high speed cutting tools, eg diamond-tipped saws.
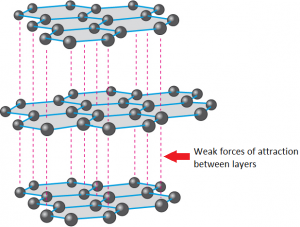
Graphite is also made of only carbon atoms, and is also a giant structure, but it is formed of layers where each carbon atom has a strong covalent bond to 3 other carbons. This means each carbon atom has one electron not involved in a covalent bond, and these electrons form a sea of delocalised electrons between the layers.
Even though it is a non-metal, graphite can conduct electricity because the delocalised electrons are free to move.
Each layer is a giant structure, with weak forces of attraction between the layers. These layers can easily slide over each other.
Graphite is soft and slippery because it has weak forces of attraction between layers. It is used as a lubricant and in pencils because it is soft and slippery.
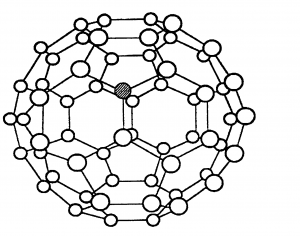
C60 fullerene which is a simple molecular structure (also known as a buckyball) is also made of only carbon atoms, but it forms molecules of 60 carbon atoms. The molecule has weak intermolecular forces of attraction between them which take little energy to overcome. Hence C60 fullerene has a low melting point, and it is soft.
C60 fullerene cannot conduct electricity. Although in each molecule every carbon is only covalently bonded to 3 others and the other electrons are delocalised, these electrons cannot jump between different molecules.
Electric current is a flow of charged particles that can move.
Covalent compounds do not conduct electricity.
When metal atoms join together the outer electrons become ‘delocalised’ which means they are free to move throughout the whole structure.
Metals have a giant regular arrangement of layers of positive ions surrounded by a sea of delocalised electrons.
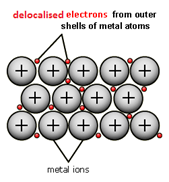
Metallic bonding is the strong electrostatic attraction between positive metal ions and a sea of delocalised electrons.

Metals are good conductors because they have delocalised electrons which are free to move.
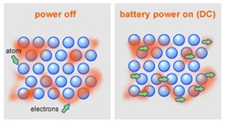
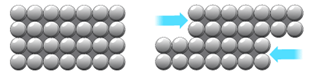
Metals are malleable (can be hammered into shape) because they have layers of ions that can slide over each other.
Electrical conductivity is the movement of charged particles.
In this case, charged particles means either delocalised electrons or ions.
These particles need to be free to move in a substance for that substance to be conductive.
Covalent compounds do not conduct electricity because there are no charged particles that are free to move.
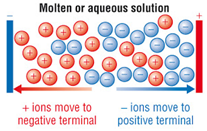
Ionic compounds only conduct electricity only when molten or in solution.
When solid the ions are not free to move.
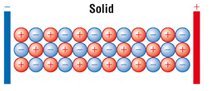
When molten or in solution the ions are free to move.
A negative ion is called an anion. Examples are the bromide ion (Br⁻) and the oxide ion (O²⁻).
A positive ion is called a cation. Examples are the sodium ion (Na⁺) and the aluminium ion (Al³⁺).
A trick to remember this is to write the ‘t’ as a ‘+’ in the word cation: ca+ion
Electrolysis: The breaking down of a substance caused by passing an electric current through an ionic compound which is molten or in solution. New substances are formed.
ELECTROLYSIS OF MOLTEN IONIC COMPOUNDS
Example: The electrolysis of molten lead bromide (PbBr2)
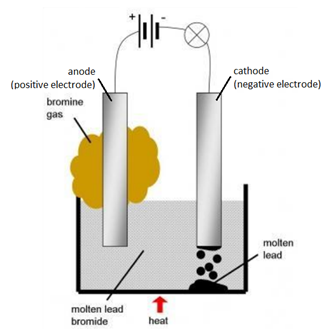
Solid lead bromide is heated and becomes molten. Explanation: ions become free to move.
Overall Reaction
word equation: lead bromide –> lead + bromine
chemical equation: PbBr2(l) –> Pb(l) + Br2(g)
Remember
OILRIG : Oxidation Is the Loss of electrons and Reduction Is the Gain of electrons
PANCAKE : Positive Anode, Negative Cathode
ELECTROLYSIS OF IONIC SOLUTIONS
Rules for working out elements formed from electrolysis of solutions
Follow these rules to decide which ions in solution will react at the electrodes:
At the cathode
Metal ions and hydrogen ions are positively charged. Whether you get the metal or hydrogen during electrolysis depends on the position of the metal in the reactivity series:
At the anode
At the anode, the product of electrolysis is always oxygen gas (O2) unless the solution contains a high concentration of Cl–, Br- or I– ions, in which case a halogen is produced, e.g. chlorine gas (Cl2), bromine gas (Br2), and iodine gas (I2).
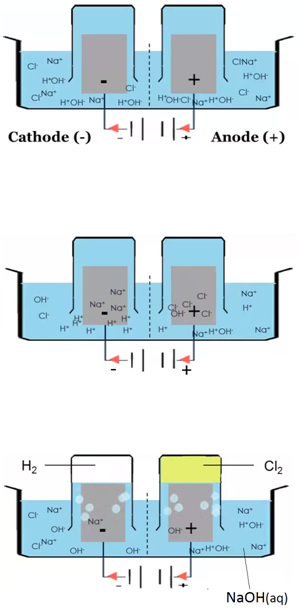
The electrolysis of sodium chloride solution (NaCl(aq))
Solid sodium chloride is dissolved in water. Explanation: The sodium ions and chloride ions become free to move.
H2O(l) ⇋ H+(aq) + OH–(aq)
Electron half equation: 2Cl–(aq) –> Cl2 (g) + 2e–
Electron half equation: 2H+(aq) + 2e– –> H2 (g)
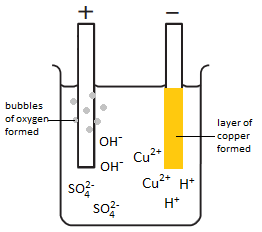
The electrolysis of copper sulfate solution (CuSO4(aq))
Electron half-equation: Cu2+(aq) + 2e– –> Cu (s)
Electron half-equation: 4OH–(aq) –> O2 (g) + 2H2O(l) + 4e–
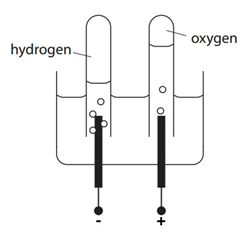
The electrolysis of sulfuric acid (H2SO4(aq))
Electron half-equation: 2H+(aq) + 2e– –> H2(g)
Electron half-equation: 4OH–(aq) –> O2 (g) + 2H2O(l) + 4e–
2H2O(l) –> 2H2(g) + O2(g)
There are twice the amount (in moles) of H2 compared to O2
Oxidation: the loss of electrons or the gain of oxygen
Reduction: the gain of electrons or the loss of oxygen
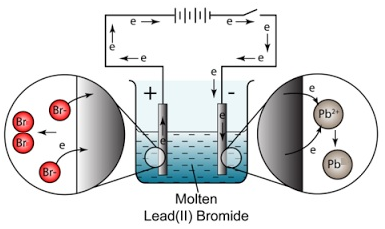
Example: The electrolysis of lead (II) bromide, PbBr2
At the cathode (negative electrode): Pb2+ (l) + 2e– → Pb (l) (reduction)
At the anode (positive electrode): 2Br– (l) → Br2 (g) + 2e– (oxidation)
Example: The electrolysis of aluminium oxide, Al2O3
At the cathode: Al3+ + 3e– → Al (reduction)
At the anode: 2O2- → O2 + 4e– (oxidation)
Example: The electrolysis of sodium chloride solution (NaCl (aq))
At the cathode: 2H+ (aq) + 2e– → H2 (g) (reduction)
At the anode: 2Cl– (aq) → Cl2 (g) + 2e– (oxidation)
Example: The electrolysis of copper sulfate solution (CuSO4 (aq))
At the cathode: Cu2+ (aq) + 2e– → Cu (s) (reduction)
At the anode: 4OH– (aq) → O2 (g) + 2H2O (l) + 4e– (oxidation)
The diagram shows an electrolytic cell.
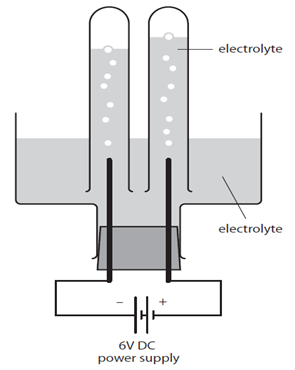
The electrolyte is an aqueous solution. For example it might be concentrated sodium chloride, NaCl (aq).
The test tubes over the electrodes must not completely cover them to make sure the ions are free to move throughout the solution.
In the case of NaCl (aq) bubbles of gas will be seen forming at the electrodes. These float up and collect in the test tubes when each gas can be tested to assess its identity.
Group 1 metals such as potassium, sodium and lithium, react with water to produce a metal hydroxide and hydrogen. For example:
lithium + water → lithium hydroxide + hydrogen
2Li (s) + 2H₂O (l) → 2LiOH (aq) + H₂ (g)
The observations for the reaction of water with either potassium or sodium or lithium have the following similarities:
In each case a metal hydroxide solution is produced.
These similarities in the reactions provide evidence that the 3 metals are in the same group of the Periodic Table (i.e. have the same number of electrons in their outer shell).
Lithium is the first element in group 1 of the Periodic Table. The observations for the reaction of lithium and water are:
Sodium is the second alkali metal in the group. The reaction of sodium and water is more vigorous than lithium’s:
Potassium is the third alkali metal in the group. The reaction of potassium and water is more vigorous than sodium’s:
When the group 1 metals react with air they oxidise, showing a similar trend in reactivity as we go down the group of the Periodic Table.
Therefore, as we go down group 1 (increasing atomic number), the elements become more reactive: Li<Na<K<Rb<Cs<Fr
From the data in the table, it is possible to deduce the properties of francium from the trends in the other group 1 metals.
For example, we can predict that francium will have a melting point around 20⁰C and a density of just over 2g/cm³.
We can also predict that francium will react violently with water, producing francium hydroxide and hydrogen.
| Alkali metal | Melting point (⁰C) | Density (g/cm³) | Reaction with water | Products |
|---|---|---|---|---|
| lithium (Li) | 181 | 0.53 | fizzing | lithium hydroxide + hydrogen |
| sodium (Na) | 98 | 0.97 | rapid fizzing | sodium hydroxide + hydrogen |
| potassium (K) | 63 | 0.86 | vigorous fizzing and lilac flame | potassium hydroxide + hydrogen |
| rubidium (Rb) | 39 | 1.53 | ? | rubidium hydroxide + hydrogen |
| caesium(Cs) | 29 | 1.88 | ? | caesium hydroxide + hydrogen |
| francium (Fr) | ? | ? | ? | ? |
As you go down the group the outer electron lost from the group 1 metal is further from the nucleus therefore the electron is less attracted by the nucleus and therefore more easily lost.
| Element | Colour | State at room temp |
|---|---|---|
| Chlorine (Cl2) | Green | Gas |
| Bromine (Br2) | Red-brown | Liquid |
| Iodine (l2) | Grey | Solid |
Chlorine is a toxic gas, so should be handled in a fume cupboard.
If you look at the trends in the physical properties of the halogens, Cl2, Br2, I2 you can make predictions about the properties of the other halogens.
| Element | Colour | State at room temp |
|---|---|---|
| Fluorine (F2) | Yellow | Gas |
| Astatine (At2) | Black | Solid |
Group 7 elements are called the Halogens. As you go up group 7 (decreasing atomic number), the elements become more reactive. For example, fluorine is the most reactive and astatine is the least reactive.
A more reactive halogen will displace a less reactive halogen, e.g. chlorine will displace bromine:

By reacting a halogen solution with a potassium halide solution and making observations, the order of their reactivity can be deduced:
| Potassium chloride, KCl(aq) | Potassium bromide, KBr(aq) | Potassium iodide, KI(aq) | |
|---|---|---|---|
| Chlorine, Cl2(aq) | No change | Colourless to orange | Colourless to brown |
| Bromine, Br2(aq) | No change | No change | Colourless to brown |
| Iodine, I2(aq) | No change | No change | No change |
From the above results, chlorine displaces both bromine and iodine, and bromine displaces iodine. Therefore the order of reactivity is: chlorine is more reactive than bromine, which in turn is more reactive than iodine.
The higher up we go in group 7 (halogens) of the periodic table, the more reactive the element. The explanation concerns how readily these elements form ions, by attracting a passing electron to fill the outer shell.
In fluorine the outer electron shell is very close to the positively charged nucleus, so the attraction between this nucleus and the negatively charged electrons is very strong. This means fluorine is very reactive indeed.
However, for iodine the outer electron shell is much further from the nucleus so the attraction is weaker. This means iodine is less reactive.
Air is a mixture of different gases.
The abundance of gases in the air is as follows:
| Gas | % by volume |
|---|---|
| Nitrogen, N2 | 78.1 |
| Oxygen, O2 | 21.0 |
| Argon, Ar | 0.9 |
| Carbon dioxide, CO2 | 0.04 |
The following 3 experiments can be used to determine that oxygen (O2) makes up approximately 20% by volume of the composition of air.
Copper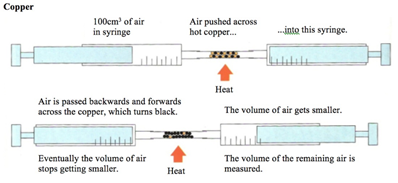
The copper is in excess and uses up the oxygen to form copper oxide (CuO).
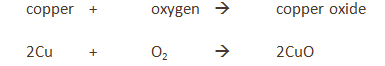
All the oxygen in the air is therefore used up, and so the volume of the air decreases by about 20% (the percentage of oxygen in air).
Iron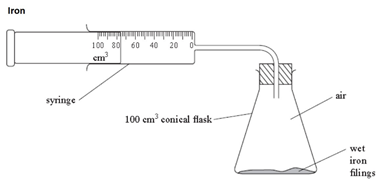
The iron reacts with the oxygen in the air (rusting).
As long as the iron and water are in excess, the total volume of air enclosed by the apparatus decreases by about a fifth (20%) over several days.
Phosphorus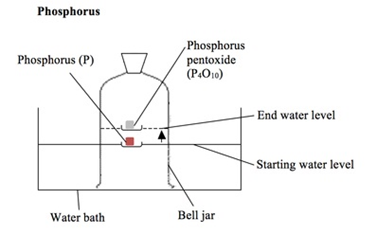
The phosphorus is lit with a hot wire.
It reacts with the oxygen in the air and causes the water level in the bell jar to rise by about 20%.