Topic: Key Calculations Archives - TutorMyself Chemistry

Key Calculations quiz

1. What is the meaning of the term Molar Volume?

The volume of 1 mole of gas at r.t.p (24 cm³ or 24,000 dm³)

The volume of 1 mole of gas at 100 ⁰C (24 cm³ or 24,000 dm³)

The volume of 1 mole of gas at 100 ⁰C (24 dm³ or 24,000 cm³)

The volume of 1 mole of gas at r.t.p (24 dm³ or 24,000 cm³)

Question 1 of 17

2. Calculate the relative formula mass(Mr) of zinc phosphide (Zn₃P₂)

120

272

223

257

Question 2 of 17

3. A beaker of 1.5 mol/dm³ calcium chloride solution contains 0.3 mol of calcium chloride. What is the volume of the solution?

0.002 dm³

4.5 dm³

0.2 dm³

0.45 dm³

Question 3 of 17

4. A graph shows the solubility of sodium chloride in water at 50°C is 34g/100g. At that temperature, what mass of sodium chloride will dissolve in 200g water?

0.68g

0.34g

68g

17g

Question 4 of 17

5. Assuming bond energies in kJ/mol: H-C 412, C-C 348, O-H 463, C-O 360, C=C 612. Calculate the molar enthalpy change for the reaction: ethanol → ethene + water

+45 kJ/mol (Some workings as follows. Breaking bonds 3231 kJ/mol. Making bonds 3186kJ/mol. Breaking - making = 3231-3186 = +45 kJ/mol)

+96 kJ/mol (Some workings as follows. Breaking bonds 1583 kJ/mol. Making bonds 1487/mol. Breaking - making = 1583-1487 = +96 kJ/mol)

-45 kJ/mol (Some workings as follows. Breaking bonds 3231 kJ/mol. Making bonds 3186kJ/mol. Making - breaking = 3186-3231 = -45 kJ/mol)

-45 kJ/mol (Some workings as follows. Breaking bonds 1583 kJ/mol. Making bonds 1487/mol. Making - breaking = 1487-1583 = -96 kJ/mol)

Question 5 of 17

6. What mass of carbon dioxide is produced when 24g of carbon undergoes completely combustion?

24 g

176 g

88g

44 g

Question 6 of 17

7. Complete the following expression: amount (in moles) =

Mᵣ / mass

Aᵣ / Mᵣ

mass / Mᵣ

amount (in moles) x Mᵣ

Question 7 of 17

8. In a combustion calorimetry experiment, 0.78g of ethanol (C₂H₅OH) produced 12,540 J of heat energy. Calculate the molar enthalpy change.

-738 kJ/mol (Amount = 0.78/46 = 0.017 mol. Answer = 12540/1000/0.017 = 738 kJ/mol)

-213 kJ/mol (Amount = 46/0.78 = 59.0 mol. Answer = 12540/59.0 = 213 kJ/mol)

-369 kJ/mol (Amount = 0.78/23 = 0.034 mol. Answer = 12540/1000/0.034 = 369 kJ/mol)

-425 kJ/mol (Amount = 23/0.78 = 29.5 mol. Answer = 12540/29.5 = 425 kJ/mol)

Question 8 of 17

9. In the thermal decomposition of calcium carbonate, we might expect 50g of calcium carbonate to produce 28g of calcium oxide. If instead only 24g of calcium oxide is produced, what is the percentage yield?

56 %

0.857 %

0.56 %

85.7 %

Question 9 of 17

10. What is the empirical formula of a compound in which 0.48 g of carbon combines with 0.08 g of hydrogen and 0.64 g of oxygen?

CH₄O

C₂H₄O₂

CH₂O

C₄H₂O

Question 10 of 17

11. Describe how to carry out an acid-alkali titration

1) Pipette 25cm³ of alkali into a conical flask. 2) Add indicator. 3) Fill a burette with acid, record the initial volume. 4) Whilst swirling the flask, add the acid dropwise until the indicator is just about to change colour. 5) Record the volume and calculate the volume of acid which was added. 6) Repeat until three concordant results (within 0.2cm³ of each other). 7) Result is the average of all concordant results.

1) Pipette 25cm³ of alkali into a conical flask. 2) Add indicator. 3) Fill a burette with acid, record the initial volume. 4) Whilst swirling the flask, add the acid dropwise until the indicator changes colour. 5) Record the volume and calculate the volume of acid which was added. 6) Repeat until three concordant results (within 0.2cm³ of each other). 7) Result is the average of all concordant results.

1) Pipette 25cm³ of alkali into a conical flask. 2) Add indicator. 3) Fill a burette with acid, record the initial volume. 4) Whilst swirling the flask, add the acid dropwise until the indicator changes colour. 5) Record the volume and calculate the volume of acid which was added. 6) Repeat until two concordant results (within 0.2cm³ of each other). 7) Result is the average of all concordant results.

1) Pipette 25cm³ of alkali into a conical flask. 2) Add indicator. 3) Fill a burette with acid, record the initial volume. 4) Whilst swirling the flask, add the acid dropwise until the indicator is just about to change colour. 5) Record the volume and calculate the volume of acid which was added. 6) Repeat until two concordant results (within 0.2cm³ of each other). 7) Result is the average of all concordant results.

Question 11 of 17

12. An oxide of nitrogen contains 26% nitrogen and 74% oxygen and has a relative molecular mass of 108. Find the empirical and molecular formulae for the oxide.

Empirical formula is NO₂.₅ Molecular formula is N₂O₅

Empirical formula is N₂O₅. Molecular formula is N₄O₁₀

Empirical formula is N₄O₁₀. Molecular formula is N₂O₅

Empirical formula is N₂O₅. Molecular formula is also N₂O₅

Question 12 of 17

13. A sample of carbon contained 98.90% carbon-12 and 1.10% carbon-13. Calculate the relative atomic mass of carbon

(12+13)/2 = 12.5

(12x13)/100 = 1.56

((13x98.90)+(12x1.10))/100 = 12.99

((12x98.90)+(13x1.10))/100 = 12.01

Question 13 of 17

14. To determine the formula of a metal oxide by combustion, magnesium is heated in a crucible. Why is a lid used?

To stop the escape of magnesium

To stop carbon dioxide escaping

To keep the magnesium warm

To stop the escape of magnesium oxide smoke

Question 14 of 17

15. What is meant by the term molecular formula?

A method of calculating the ratios of masses in an equation

A method of calculating the mass needed to make a certain yield in an equation

A chemical formula that shows the actual numbers of the different types of atoms in a molecule

A chemical formula that shows the simplest ratio of the numbers of atoms in a compound

Question 15 of 17

16. Use Q=mcΔT and c=4.18J/°C/g. 25cm³ of sulfuric acid is put into a boiling tube. The starting temperature is 21°C. A spatula of iron filings is added. After a while the temperature reaches 33°C. What is the total heat energy change?

3383 J

2153 J

2.153 kJ

1254 J

Question 16 of 17

17. What are the units for amount in Chemistry?

Grams

mol/dm³

Moles

g per 100g of solvent

Question 17 of 17

Hydr0Gen2020-02-16T17:35:16+00:00Categories: Uncategorized|Tags: Quiz, Topic: Key Calculations|

Flashcards: Key Calculations

Key calculations (Triple) flashcards

Key calculations (Double) flashcards

Hydr0Gen2019-08-28T16:53:21+00:00Categories: Uncategorized|Tags: Chemistry, Flashcards, GCSE, Topic: Key Calculations|

Q&A slides – Key Calculations

Hydr0Gen2019-11-12T07:38:38+00:00Categories: Uncategorized|Tags: Chemistry, GCSE, Q&A slides, Topic: Key Calculations|

Calculations practice – Molecular formulae

Refresh the page to get a different random selection of questions and answers.

Hydr0Gen2019-11-12T07:57:17+00:00Categories: Uncategorized|Tags: CalcPractice, Chemistry, GCSE, Topic: Calculations, Topic: Key Calculations|

Calculations practice – Reacting masses

Refresh the page to get a different random selection of questions and answers.

Hydr0Gen2019-11-12T08:45:26+00:00Categories: Uncategorized|Tags: CalcPractice, Chemistry, GCSE, Topic: Key Calculations|

Calculations practice – Mixed calculations

Refresh the page to get a different random selection of questions and answers.

Hydr0Gen2019-11-12T07:57:45+00:00Categories: Uncategorized|Tags: CalcPractice, Chemistry, GCSE, Topic: Key Calculations|

mass = Mr x moles

Hydr0Gen2019-05-13T15:10:29+00:00Categories: Uncategorized|Tags: Chemistry, GCSE, otherPost, Topic: Key Calculations, Topic: Moles|

1:06 (Triple only) understand how to plot and interpret solubility curves

The solubility of solids changes as temperature changes. This can be plotted on a solubility curve.

The salts shown on this graph are typical: the solubility increases as temperature increases.

For example, the graph above shows that in 100g of water at 50⁰C the maximum mass of potassium nitrate (KNO₃) which will dissolve is 80g.

However, if the temperature were 80⁰C a mass of 160g of potassium nitrate (KNO₃) would dissolve in 100g of water.

Hydr0Gen2023-09-18T10:59:46+00:00Categories: (a) States of matter, 1 Principles of chemistry, Edexcel iGCSE Chemistry|Tags: 1:06, Chemistry, ChemistrySpecPointsNew2019, GCSE, GCSE_Chemistry_SpecPoint, SpecPoint, Topic: Key Calculations, Topic: Simple Molecules & Covalent Bonding, Triple|

1:17 be able to calculate the relative atomic mass of an element (Aᵣ) from isotopic abundances

75% of chlorine atoms are the type ³⁵Cl (have a mass number of 35)

25% of chlorine atoms are of the type ³⁷Cl (have a mass number of 37)

In order to calculate the relative atomic mass (A_r) of chlorine, the following steps are used:

Multiply the mass of each isotope by its relative abundance
Add those together
Divide by the sum of the relative abundances (normally 100)

$A_r = \frac{( (35 \times 75) + (37 \times 25) )}{100}$

$A_r = 35.5$

Example question:

A sample of bromine contained the two isotopes in the following proportions: bromine-79 = 50.7% and bromine-81 = 49.3%.

Calculate the relative atomic mass (A_r) of bromine.

$A_r = \frac{( (79 \times 50.7) + (81 \times 49.3) )}{100}$

$A_r = 79.99$

Hydr0Gen2022-11-30T14:11:27+00:00Categories: (c) Atomic structure, 1 Principles of chemistry, Edexcel iGCSE Chemistry|Tags: 1:17, Chemistry, Double, GCSE, GCSE_Chemistry_Single, GCSE_Chemistry_SpecPoint, SpecPoint, Topic: Calculations, Topic: Key Calculations|

Calculation of relative atomic mass – Tyler de Witt video

This excellent video from Tyler de Witt walks you through what isotopes are, and how the relative abundance of those isotopes can be used to calculate the relative atomic mass of an element.

Hydr0Gen2019-02-10T11:44:48+00:00Categories: Uncategorized|Tags: Chemistry, GCSE, Topic: Calculations, Topic: Key Calculations, Video|

1:26 calculate relative formula masses (including relative molecular masses) (Mᵣ) from relative atomic masses (Aᵣ)

Relative formula mass (M_r) is mass of a molecule or compound (on a scale compared to carbon-12).

It is calculated by adding up the relative atomic masses (A_r) of all the atoms present in the formula.

Example:

The relative formula mass (M_r) for water (H₂O) is 18.

Water = H₂O

Atoms present = (2 x H) + (1 x O)

M_r = (2 x 1) + (1 x 16) = 18

Hydr0Gen2022-11-30T14:12:46+00:00Categories: (e) Chemical formulae, equations and calculations, 1 Principles of chemistry, Edexcel iGCSE Chemistry|Tags: 1:26, Chemistry, Double, GCSE, GCSE_Chemistry_Single, GCSE_Chemistry_SpecPoint, SpecPoint, Topic: Calculations, Topic: Fundamentals, Topic: Key Calculations, Topic: Moles|

Calculation of relative formula mass – Tyler de Witt video

Here’s an excellent Tyler de Witt video explaining how to calculate the relative formula mass of compounds with:

a simple formula
a formula which includes brackets
a formula which includes a dot (water of crystallisation)

Hydr0Gen2019-02-10T12:17:13+00:00Categories: Uncategorized|Tags: Chemistry, GCSE, Topic: Calculations, Topic: Fundamentals, Topic: Key Calculations, Topic: Moles, Video|

1:27 know that the mole (mol) is the unit for the amount of a substance

In Chemistry, the mole is a measure of amount of substance (n).

The abbreviation for mole is mol.

The mass of 1 mole of a substance is the relative formula mass (M_r) of the substance in grams.

Example:

The M_r of water is 18.

Therefore the mass of 1 mol of water equals 18 g.

Hydr0Gen2018-04-25T21:37:27+00:00Categories: (e) Chemical formulae, equations and calculations, 1 Principles of chemistry, Edexcel iGCSE Chemistry|Tags: 1:27, Chemistry, Double, GCSE, GCSE_Chemistry_SpecPoint, SpecPoint, Topic: Key Calculations, Topic: Moles|

1:28 understand how to carry out calculations involving amount of substance, relative atomic mass (Aᵣ) and relative formula mass (Mᵣ)

The following formula allows for the interconversion between a mass in grams and a number of moles for a given substance:

$Amount(mol) = \frac{mass(g)}{M_r}$

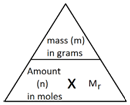
Example 1:

Calculate the amount, in moles, of 8.8 g of carbon dioxide (CO₂).

Step 1: Calculate the relative formula mass (M_r) of carbon dioxide (CO₂).

$Carbon\,dioxide = CO_2$

$Atoms\,present = (1 \times C) + (2 \times O)$

$M_r = (1 \times 12) + (2 \times 16) = 44$

Step 2: Use the formula to calculate the amount in moles.

$Amount = \frac{mass(g)}{M_r}$

$Amount = \frac{8.8}{44}$

$Amount = 0.2 mol$

Example 2:

Calculate the mass of 2 mol of copper(II) sulfate (CuSO₄).

Step 1: Calculate the relative formula mass (M_r) of copper(II) sulfate (CuSO₄).

$copper(II)\,sulfate = CuSO_4$

$Atoms\,present = (1 \times Cu) + (1 \times S) + (4 \times O)$

$M_r = (1 \times 63.5) + (1 \times 32) + (4 \times 16) = 159.5$

Step 2: Rearrange the formula to calculate the mass.

$mass = amount \times M_r$

$mass = 2 \times 159.5$

$mass = 319g$

Hydr0Gen2018-04-25T21:37:27+00:00Categories: (e) Chemical formulae, equations and calculations, 1 Principles of chemistry, Edexcel iGCSE Chemistry|Tags: 1:28, Chemistry, Double, GCSE, GCSE_Chemistry_SpecPoint, SpecPoint, Topic: Key Calculations, Topic: Moles|

Calculations involving mass (in grams), amount (in moles) and relative atomic mass – Tyler de Witt video

This video shows how to perform calculations involving mass (in grams), amount (in moles) and relative atomic mass:

Hydr0Gen2019-02-10T14:19:00+00:00Categories: Uncategorized|Tags: Chemistry, GCSE, Topic: Calculations, Topic: Key Calculations, Topic: Moles, Video|

1:29 calculate reacting masses using experimental data and chemical equations

Example: When calcium carbonate (CaCO₃) is heated calcium oxide is produced. You can use reacting mass calculations to calculate the mass of calcium oxide produced when heating 25 g of calcium carbonate.

CaCO₃ –> CaO + CO₂

Step 1: Calculate the amount, in moles, of 25 g of calcium carbonate (CaCO₃)

$M_r(CaCO_3)=(1 \times 40) + (1\times12) + (3 \times 16)$

$M_r(CaCO_3)= 100$

$Amount = \frac{mass(g)}{M_r}$

$Amount = \frac{25}{100}$

$Amount = 0.25 mol$

Step 2: Deduce the amount, in moles, of CaO produced from 0.25 mol of CaCO₃.

This step involves using the ratio of CaCO₃ to CaO from the chemical equation.

CaCO₃ –> CaO + CO₂

From the equation you can see that the ratio of CaCO₃ to CaO is 1:1.

Therefore if you have 0.25 mol of CaCO₃ this will produced 0.25 mol of CaO.

Step 3: Calculate the mass of 0.25 mol of CaO.

$M_r(CaO)=(1 \times 40) + (1 \times 16)$

$M_r(CaO)= 56$

$Mass(CaO)=amount \times M_r$

$Mass(CaO)= 0.25 \times 56$

$Mass(CaO)= 14g$

A simple format for laying out this method can be used.

Example: What mass of ammonia (NH₃) is formed when 7 g of nitrogen (N₂) is combined with hydrogen (H₂).

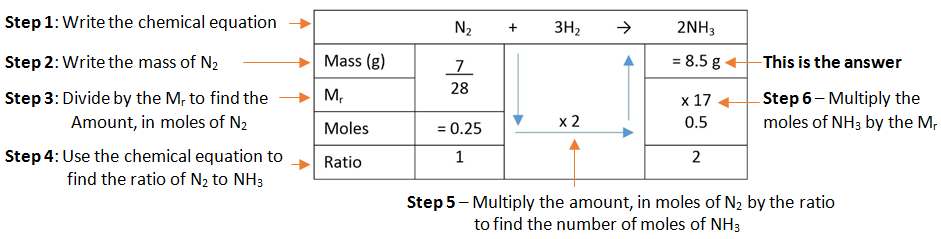
Hydr0Gen2018-04-25T21:37:27+00:00Categories: (e) Chemical formulae, equations and calculations, 1 Principles of chemistry, Edexcel iGCSE Chemistry|Tags: 1:29, Chemistry, Double, GCSE, GCSE_Chemistry_SpecPoint, SpecPoint, Topic: Key Calculations, Topic: Moles|

Calculate Reacting Masses video

This video steps through a very useful method used to calculate reacting masses.

Hydr0Gen2020-02-07T14:47:28+00:00Categories: Uncategorized|Tags: Chemistry, GCSE, Topic: Key Calculations, Topic: Moles, Video|

1:30 calculate percentage yield

Yield is how much product you get from a chemical reaction.

The theoretical yield is the amount of product that you would expect to get. This is calculated using reacting mass calculations.

In most chemical reactions, however, you rarely achieved your theoretical yield.

For example, in the following reaction:

CaCO₃ –> CaO + CO₂

You might expect to achieve a theoretical yield of 56 g of CaO from 100 g of CaCO₃.

However, what if the actual yield is only 48 g of CaO.

By using the following formula, the % yield can be calculated:

$yield= \frac{actual\,amount\,of\,product}{theoretical\,amount\,of\,product}$

$yield= \frac{48}{56}$

$yield=0.86$

$\% yield=86\%$

Hydr0Gen2023-01-10T11:13:31+00:00Categories: (e) Chemical formulae, equations and calculations, 1 Principles of chemistry, Edexcel iGCSE Chemistry|Tags: 1:30, Chemistry, Double, GCSE, GCSE_Chemistry_SpecPoint, SpecPoint, Topic: Equilibria, Topic: Key Calculations, Topic: Reversible Reactions (D)|

1:31 understand how the formulae of simple compounds can be obtained experimentally, including metal oxides, water and salts containing water of crystallisation

Finding the formula of a metal oxide experimentally

The formulae of metal oxides can be found experimentally by reacting a metal with oxygen and recording the mass changes.

Example: When magnesium is burned in air, it reacts with oxygen (O₂) to form magnesium oxide (MgO).

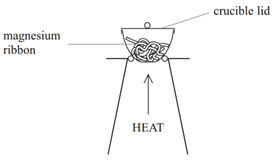
Method:
• Weigh a crucible and lid
• Place the magnesium ribbon in the crucible, replace the lid, and reweigh
• Calculate the mass of magnesium
(mass of crucible + lid + Magnesium – mass of crucible + lid)
• Heat the crucible with lid on until the magnesium burns
(lid prevents magnesium oxide escaping therefore ensuring accurate results)
• Lift the lid from time to time (this allows air to enter)
• Stop heating when there is no sign of further reaction
(this ensures all Mg has reacted)
• Allow to cool and reweigh
• Repeat the heating , cooling and reweigh until two consecutive masses are the same
(this ensures all Mg has reacted and therefore the results will be accurate)
• Calculate the mass of magnesium oxide formed (mass of crucible + lid + Magnesium oxide – mass of crucible + lid)

Finding the formula of a salt containing water of crystallisation

When some substances crystallise from solution, water becomes chemically bound up with the salt. This is called water of crystallisation and the salt is said to be hydrated. For example, hydrated copper sulfate has the formula CuSO₄.5H₂O which formula indicates that for every CuSO₄ in a crystal there are five water (H₂O) molecules.

When you heat a salt that contains water of crystallisation, the water is driven off leaving the anhydrous (without water) salt behind. If the hydrated copper sulfate (CuSO₄.5H₂O) are strongly heated in a crucible then they will break down and the water lost, leaving behind anhydrous copper sulfate (CuSO₄). The method followed is similar to that for metal oxides, as shown above. The difference of mass before and after heating is the mass of the water lost. These mass numbers can be used to obtain the formula of the salt.

Hydr0Gen2023-01-10T11:36:41+00:00Categories: (e) Chemical formulae, equations and calculations, 1 Principles of chemistry, Edexcel iGCSE Chemistry|Tags: 1:31, Chemistry, Double, GCSE, GCSE_Chemistry_SpecPoint, SpecPoint, Topic: Acids & Salts, Topic: Acids & Salts (D), Topic: Key Calculations, Topic: Specification experiments|

1:32 know what is meant by the terms empirical formula and molecular formula

The empirical formula shows the simplest whole-number ratio between atoms/ions in a compound.

The molecular formula shows the actual number of atoms of each type of element in a molecule.

For example, for ethane:

Molecular formula = C₂H₆

Empirical formula = CH₃

Here are some more examples:

Name	Molecular formula	Empirical Formula
pentene	C₅H₁₀	CH₂
butene	C₄H₈	CH₂
glucose	C₆H₁₂O₆	CH₂O
hydrogen peroxide	H₂O₂	HO
propane	C₃H₈	C₃H₈

Notice from the table that several different molecules can have the same empirical formula, which means that it is not possible to deduce the molecular formula from the empirical formula without some additional information. Also notice that sometimes it is not possible to simplify a molecular formula into simpler whole-number ratio, in which case the empirical formula is equal to the molecular formula.

Hydr0Gen2023-01-10T08:29:26+00:00Categories: (e) Chemical formulae, equations and calculations, 1 Principles of chemistry, Edexcel iGCSE Chemistry|Tags: 1:32, Chemistry, Double, GCSE, GCSE_Chemistry_SpecPoint, SpecPoint, Topic: Calculations, Topic: Crude oil to plastics (D), Topic: Key Calculations|

1:33 calculate empirical and molecular formulae from experimental data

Calculating the Empirical Formula

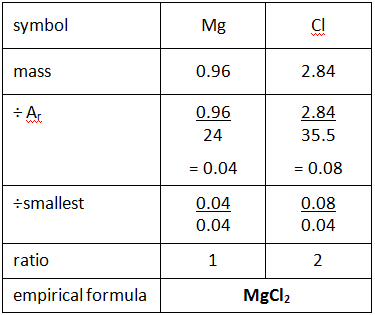Example: What is the empirical formula of magnesium chloride if 0.96 g of magnesium combines with 2.84 g of chlorine?

Step 1: Put the symbols for each element involved at the top of the page.

Step 2: Underneath, write down the masses of each element combining.

Step 3: Divide by their relative atomic mass (A_r).

Step 4: Divide all the numbers by the smallest of these numbers to give a whole number ratio.

Step 5: Use this to give the empirical formula.

(If your ratio is 1:1.5 then multiple each number by 2

If your ratio is 1:1.33 then x3. If your ratio is 1:1.25 x4)

Calculating the Molecular Formula

If you know the empirical formula and the relative formula mass you can work out the molecular formula of a compound.

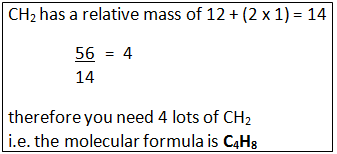
Example: A compound has the empirical formula CH₂, and its relative formula mass is 56. Calculate the molecular formula.

Step 1: Calculate the relative mass of the empirical formula.

Step 2: Find out the number of times the relative mass of the empirical formula goes into the M_r of the compound.

Step 3: This tells how many times bigger the molecule formula is compared to the empirical formula.

Empirical formula calculations involving water of crystallisation

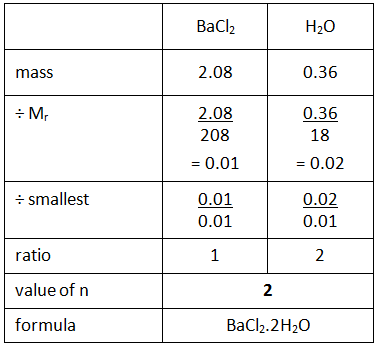
When you heat a salt that contains water of crystallisation, the water is driven off leaving the anhydrous (without water) salt behind. For example, barium chloride crystals contain water of crystallisation, and therefore would have the formula BaCl₂.nH₂O where the symbol ‘n’ indicates the number of molecules of water of crystallisation. This value can be calculated using the following method.

Example: If you heated hydrated barium chloride (BaCl₂.nH₂O) in a crucible you might end up with the following results.

Step 1: Calculate the mass of the anhydrous barium chloride (BaCl₂) and the water (H₂O) driven off.

Step 2: Use the empirical formula method to find the value of n in the formula.

Hydr0Gen2023-01-10T08:30:04+00:00Categories: (e) Chemical formulae, equations and calculations, 1 Principles of chemistry, Edexcel iGCSE Chemistry|Tags: 1:33, Chemistry, Double, GCSE, GCSE_Chemistry_SpecPoint, SpecPoint, Topic: Calculations, Topic: Crude oil to plastics (D), Topic: Key Calculations|

Empirical formula calculation example

Hydr0Gen2020-02-08T11:17:29+00:00Categories: Uncategorized|Tags: Topic: Calculations, Topic: Key Calculations, Video|

Empirical formulae and Molecular formulae – Tyler de Witt video

In this video, the lovely Tyler de Witt explains Empirical Formulae and Molecular formulae.

(Please excuse the horrid error right at the start where the video shows a diagram of prop-2-ene, but it is labelled ‘ethene’ by mistake.)

This second video then explains how, if given an empirical formula and a molecular mass, you can calculate the molecular formula:

Hydr0Gen2019-02-10T14:09:31+00:00Categories: Uncategorized|Tags: Chemistry, GCSE, Topic: Calculations, Topic: Key Calculations, Video|

1:34 (Triple only) understand how to carry out calculations involving amount of substance, volume and concentration (in mol/dm³) of solution

Concentration is a measurement of the amount of substance per unit volume.

In Chemistry, concentration is measured in mol/dm³ (read as moles per cubic decimetre).

The following formula allows for the interconversion between a concentration (in mol/dm³), the amount (in moles) of a substance in a solution, and the volume of the solution (in dm³).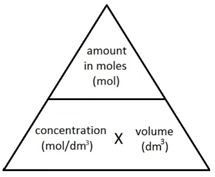

$amount(mol) = concentration(mol/dm^3) \times volume(dm^3)$

or

$concentration(mol/dm^3) = \frac{amount(mol)}{volume(dm^3)}$

Note: 1 dm³ = 1000 cm³

For example, to convert 250 cm³ into dm³:

$250cm^3 = \frac{250}{1000}$

$250cm^3 = 0.25dm^3$

Example 1: 0.03 mol of sodium carbonate (Na₂CO₃) is dissolved in 300 cm³ of water. Calculate the concentration of the solution.

Step 1: Convert the volume of water from cm³ into dm³.

$volume = 300cm^3$

$volume = \frac{300}{1000}dm^3$

$volume = 0.300dm^3$

Step 2: Use the molar concentration formula to calculate of the concentration of the solution.

$concentration = \frac{amount}{volume}$

$concentration = \frac{0.03}{0.300}$

$concentration = 0.1 mol/dm^3$

Example 2: Calculate the amount, in moles, of 25cm³ of hydrochloric acid (HCl) with a concentration of 2 mol/dm³.

Step 1: Convert the volume of HCl from cm³ into dm³.

$volume = 25cm^3$

$volume = \frac{25}{1000}dm^3$

$volume = 0.025dm^3$

Step 2: Rearrange the molar concentration formula to calculate of the amount, in moles of HCl.

$amount= concentration \times volume$

$amount = 2 \times 0.025$

$amount = 0.050 mol$

Titration calculations, example 1

The titration method that is used to prepare a soluble salt is also used to determine the concentration of an unknown solution.

For example, a titration problem will look like this:

A pupil carried out a titration to find the concentration of a solution of hydrochloric acid (HCl). She found that 25.0 cm³ of 0.100 mol/dm³ sodium hydroxide solution (NaOH) required 23.50 cm³ of dilute hydrochloric acid for neutralisation. Calculate the concentration, in mol/dm³ of the acid.

The chemical equation for this reaction is:

NaOH(aq) + HCl(aq) –> NaCl(aq) + H₂O(l)

volume 25.0cm³ 23.50cm³

concentration 0.100mol/dm³

It can be useful, as shown above, to write the values of the volumes & concentration underneath the equation.

Step 1: Calculate the amount, in moles, of the solution that you know the values for both volume and concentration. In this case sodium hydroxide (NaOH).

First convert the volume of NaOH from cm³ into dm³.

$volume = 25cm^3$

$volume = \frac{25}{1000}dm^3$

$volume = 0.025dm^3$

Then rearrange the molar concentration formula to calculate of the amount, in moles of NaOH.

$amount= concentration \times volume$

$amount = 0.100 \times 0.025$

$amount = 0.0025 mol$

Step 2: Deduce the amount, in moles of the solution with the unknown concentration. In this case hydrochloric acid (HCl).

From the chemical equation the ratio of NaOH to HCl is 1:1

Therefore if you have 0.0025 mol of NaOH, this will react with 0.0025 mol of HCl.

Step 3: Calculate the concentration of the hydrochloric acid (HCl).

Convert the volume of HCl from cm³ into dm³.

$volume = 23.5cm^3$

$volume = \frac{23.5}{1000}dm^3$

$volume = 0.0235dm^3$

Use the molar concentration formula to calculate of the concentration of the HCl.

$concentration = \frac{amount}{volume}$

$concentration = \frac{0.0025}{0.0235}$

$concentration = 0.106 mol/dm^3$

Titration calculations, example 2

25.0 cm³ of sodium carbonate solution (Na₂CO₃) of unknown concentration was neutralised by 30.0 cm³ of 0.100 mol/dm³ nitric acid (HNO₃).

Na₂CO₃(aq) + 2HNO₃(aq) –> 2NaNO₃(aq) + CO₂(g) + H₂O(l)

Calculate the concentration, in mol/dm³ of the sodium carbonate solution.

Step 1: Calculate the amount, in moles, of nitric acid (HNO₃).

$volume = 30cm^3$

$volume = \frac{30}{1000}dm^3$

$volume = 0.030dm^3$

$amount= concentration \times volume$

$amount = 0.100 \times 0.030$

$amount = 0.0030 mol$

Step 2: Deduce the amount, in moles of sodium carbonate (Na₂CO₃).

Using the equation:

Na₂CO₃(aq) + 2HNO₃(aq) –> 2NaNO₃(aq) + CO₂(g) + H₂O(l)

Ratio Na₂CO₃:HNO₃ = 1:2

$amount=\frac{0.0030}{2} = 0.0015mol$

Step 3: Calculate the concentration of sodium carbonate (Na₂CO₃).

$volume = 25cm^3$

$volume = \frac{25}{1000}dm^3$

$volume = 0.025dm^3$

$concentration = \frac{amount}{volume}$

$concentration = \frac{0.0015}{0.025}$

$concentration = 0.06 mol/dm^3$

Converting mol/dm³ into g/dm³

Concentration can also be expressed in g/dm³ (grams per cubic decimetre).

Therefore mol/dm³ can be converted into g/dm³.

Example: Convert 0.06 mol/dm³ of sodium carbonate (Na₂CO₃) into g/dm³

Step 1: calculate the relative formula mass (M_r) of sodium carbonate (Na₂CO₃).

$M_r= (2 \times 23) + (1 \times 12) (3 \times 16) = 106$

Step 2: Recall the formula giving the relationship between mass, amount and formula mass.

$mass= amount(in\,moles) \times M_r$

therefore

$mass/dm^3= moles/dm^3 \times M_r$

$mass/dm^3= 0.06 \times 106$

$mass/dm^3= 6.36 g/dm^3$

Hydr0Gen2019-05-13T15:41:32+00:00Categories: (e) Chemical formulae, equations and calculations, 1 Principles of chemistry, Edexcel iGCSE Chemistry|Tags: 1:34, Chemistry, GCSE, GCSE_Chemistry_SpecPoint, SpecPoint, Topic: Key Calculations, Triple|

Titration calculation example

Hydr0Gen2020-02-08T10:42:04+00:00Categories: Uncategorized|Tags: Topic: Key Calculations, Video|

Concentration (molarity) practice problems – Tyler de Witt video

Here is a video to help you with concentration calculations. In Chemistry, concentration is know as molarity (i.e. the amount per volume).

Note that in the video, the lovely Tyler de Witt uses the unit “liter” for volume, but the correct international unit (as used by UK exam boards) is decimeters cubed (dm³) which is the same thing as Tyler’s “liter”.

and a follow up video with some more examples:

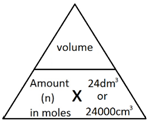
Hydr0Gen2019-02-10T14:51:45+00:00Categories: Uncategorized|Tags: Chemistry, GCSE, Topic: Key Calculations, Video|

1:35 (Triple only) understand how to carry out calculations involving gas volumes and the molar volume of a gas (24dm³ and 24,000cm³ at room temperature and pressure (rtp))

The molar volume of a gas is the volume that one mole of any gas will occupy.

1 mole of gas, at room temperature and pressure (rtp), will always occupy 24 dm³ or 24,000 cm³.

Note: 1 dm³ = 1000 cm³

The following formulae allows for the interconversion between a volume in dm³ or cm³ and a number of moles for a given gas:

$Amount(mol) = \frac{volume(dm^3)}{24}$

or

$Amount(mol) = \frac{volume(cm^3)}{24000}$

Example 1:

Calculate the amount, in moles, of 12 dm³ of carbon dioxide (CO₂).

$Amount = \frac{volume(dm^3)}{24}$

$Amount = \frac{12}{24}$

$Amount = 0.5mol$

Example 2:

Calculate the volume at rtp in cubic centimetres (cm³), of 3 mol of oxygen, (O₂).

$Volume = amount \times 24000$

$Volume = 3 \times 24000$

$Volume = 72000cm^3$

Hydr0Gen2019-06-21T14:38:23+00:00Categories: (e) Chemical formulae, equations and calculations, 1 Principles of chemistry, Edexcel iGCSE Chemistry|Tags: 1:35, Chemistry, GCSE, GCSE_Chemistry_SpecPoint, SpecPoint, Topic: Key Calculations, Triple|

1:36 practical: know how to determine the formula of a metal oxide by combustion (e.g. magnesium oxide) or by reduction (e.g. copper(II) oxide)

To determine the formula of a metal oxide by combustion.

Example: When magnesium is burned in air, it reacts with oxygen (O₂) to form magnesium oxide (MgO).

2Mg + O₂ –> 2MgO

Method:

Weigh a crucible and lid
Place the magnesium ribbon in the crucible, replace the lid, and reweigh
Calculate the mass of magnesium
Heat the crucible with lid on until the magnesium burns (lid prevents magnesium oxide escaping therefore ensuring accurate results)
Lift the lid from time to time (this allows air to enter)
Stop heating when there is no sign of further reaction
Allow to cool and reweigh
Repeat the heating, cooling and reweigh until two consecutive masses are the same (this ensures all Mg has reacted and therefore the results will be accurate)
Calculate the mass of magnesium oxide formed (mass after heating – mass of crucible)

It is then possible to use this data to calculate the empirical formula of the metal oxide.

To determine the formula of a metal oxide by reduction

Example: When copper (II) oxide is heated in a stream of methane, the oxygen is removed from the copper (II) oxide, producing copper, carbon dioxide and water:

4CuO + CH₄ –> 4Cu + CO₂ + 2H₂O

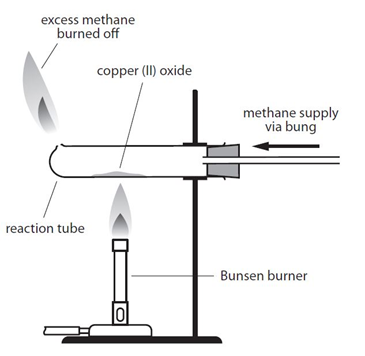
By comparing the mass of copper produced with the mass of copper oxide used it is possible to determine the formula of the copper oxide.

As an alternative, hydrogen gas could be used instead of methane:

CuO + H₂ –> Cu + H₂O

It is then possible to use this data to calculate the empirical formula of the metal oxide.

There is an important safety point to note with both versions of this experiment. Both methane and hydrogen are explosive if ignited with oxygen. It is important that a good supply of the the gas is allowed to fill the tube before the gas it lit. This flushes out any oxygen from the tube, so the gas will only burn when it exits the tube and comes into contact with oxygen in the air.

Hydr0Gen2019-03-16T10:58:55+00:00Categories: (e) Chemical formulae, equations and calculations, 1 Principles of chemistry, Edexcel iGCSE Chemistry|Tags: 1:36, Chemistry, Double, GCSE, GCSE_Chemistry_SpecPoint, SpecPoint, Topic: Calculations, Topic: Key Calculations, Topic: Specification experiments|

2:33 (Triple only) describe how to carry out an acid-alkali titration

Titration is used to find out precisely how much acid neutralises a certain volume of alkali (or vice versa).

The diagram shows the titration method for a neutralisation reaction between hydrochloric acid and sodium hydroxide, using phenolphthalein as an indicator. The indicator changes colour when neutralisation occurs.

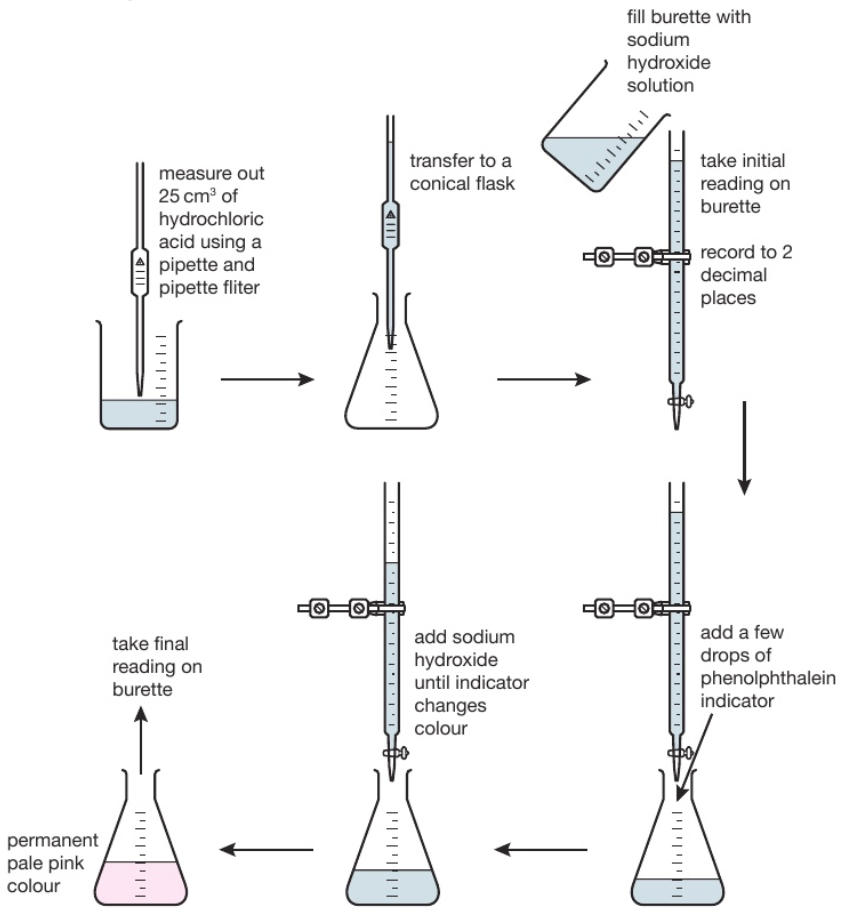
The conical flask is swirled to mix the solutions each time alkali is added. When reading the burette it is important to be aware that the numbers on the scale increase from top to bottom. Readings are usually recorded to the nearest 0.05cm³ so all readings should be written down with 2 decimal places. The second decimal place is given as a ‘0’ if the level of the solution is on a line, or ‘5’ if it is between the lines. The volume of alkali added is calculated by subtracting the final reading from the initial reading. Various indicators can be used such as phenolphthalein or methyl orange. However universal indicator should not be used since it has a wide range of colours rather than one specific colour change so it would be unclear when the precise endpoint of titration was achieved.

This process is repeated a number of times. The first time it is done roughly to get a good approximation of how much alkali needs to be added. On subsequent attempts, the alkali is added very slowly when approaching the correct volume.

Hydr0Gen2019-05-13T15:37:44+00:00Categories: (f) Acids, alkalis and titrations, 2 Inorganic chemistry, Edexcel iGCSE Chemistry|Tags: 2:33, Chemistry, GCSE, GCSE_Chemistry_SpecPoint, SpecPoint, Topic: Key Calculations, Topic: Specification experiments, Triple|

(Triple only) Titration calculations – videos

Here are a couple of videos explaining how to perform titration calculations:

Hydr0Gen2019-02-10T16:02:41+00:00Categories: Uncategorized|Tags: Chemistry, GCSE, Topic: Key Calculations, Video|

3:03 calculate the heat energy change from a measured temperature change using the expression Q = mcΔT

Calorimetry allows for the measurement of the amount of energy transferred in a chemical reaction to be calculated.

EXPERIMENT1: Displacement, dissolving and neutralisation reactions

Example: magnesium displacing copper from copper(II) sulfate

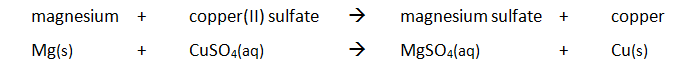
Method:

50 cm³ of copper(II) sulfate is measured and transferred into a polystyrene cup.
The initial temperature of the copper sulfate solution is measured and recorded.
Magnesium is added and the maximum temperature is measured and recorded.
The temperature rise is then calculated. For example:

Initial temp. of solution (^oC)	Maximium temp. of solution (^oC)	Temperature rise (^oC)
24.2	56.7	32.5

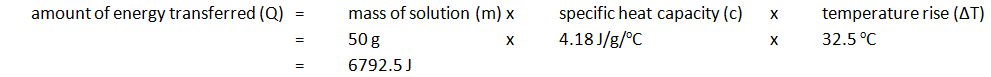
Note: mass of 50 cm³ of solution is 50 g

EXPERIMENT2: Combustion reactions

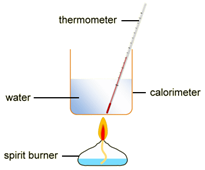
To measure the amount of energy produced when a fuel is burnt, the fuel is burnt and the flame is used to heat up some water in a copper container

Example: ethanol is burnt in a small spirit burner

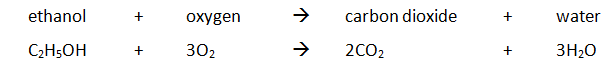
Method:

The initial mass of the ethanol and spirit burner is measured and recorded.
100cm³ of water is transferred into a copper container and the initial temperature is measured and recorded.
The burner is placed under of copper container and then lit.
The water is stirred constantly with the thermometer until the temperature rises by, say, 30 ^oC
The flame is extinguished and the maximum temperature of the water is measured and recorded.
The burner and the remaining ethanol is reweighed. For example:

Mass of water (g)	Initial temp of water (^oC)	Maximum temp of water (^oC)	Temperature rise (^oC)	Initial mass of spirit burner + ethanol (g)	Final mass of spirit burner + ethanol (g)	Mass of ethanol burnt (g)
100	24.2	54.2	30.0	34.46	33.68	0.78

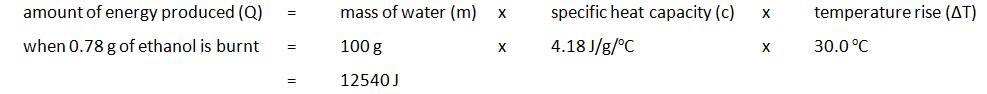
The amount of energy produced per gram of ethanol burnt can also be calculated:

Hydr0Gen2023-03-06T17:22:19+00:00Categories: (a) Energetics, 3 Physical chemistry, Edexcel iGCSE Chemistry|Tags: 3:03, Chemistry, Double, GCSE, GCSE_Chemistry_Single, GCSE_Chemistry_SpecPoint, SpecPoint, Topic: Crude oil to plastics (D), Topic: Energetics, Topic: Energetics (D), Topic: Key Calculations|

3:04 calculate the molar enthalpy change (ΔH) from the heat energy change, Q

Hydr0Gen2023-01-10T11:59:12+00:00Categories: (a) Energetics, 3 Physical chemistry, Edexcel iGCSE Chemistry|Tags: 3:04, Chemistry, Double, GCSE, GCSE_Chemistry_SpecPoint, SpecPoint, Topic: Crude oil to plastics (D), Topic: Energetics, Topic: Energetics (D), Topic: Key Calculations|

3:07 (Triple only) use bond energies to calculate the enthalpy change during a chemical reaction

Each type of chemical bond has a particular bond energy. The bond energy can vary slightly depending what compound the bond is in, therefore average bond energies are used to calculate the change in heat (enthalpy change, ΔH) of a reaction.

Example: dehydration of ethanol

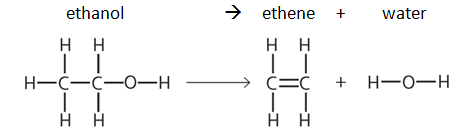
Note: bond energy tables will always be given in the exam, e.g:

Bond	Average bond energy in kJ/mol
H-C	412
C-C	348
O-H	463
C-O	360
C=C	612

So the enthalpy change in this example can be calculated as follows:

Breaking bonds		Making bonds
Bonds	Energy (kJ/mol)	Bonds	Energy (kJ/mol)
H-C x 5	(412 x 5) = 2060	C-H x 4	(412 x 4) = 1648
C-C	348	C=C	612
C-O	360	O-H x 2	(463 x 2) = 926
O-H	463
Energy needed to break all the bonds	3231	Energy released to make all the new bonds	3186
Enthalpy change, ΔH = Energy needed to break all the bonds - Energy released to make all the new bonds ΔH = 3231 – 3186 = +45 kJ/mol (ΔH is positive so the reaction is endothermic)

Hydr0Gen2019-05-13T15:36:47+00:00Categories: (a) Energetics, 3 Physical chemistry, Edexcel iGCSE Chemistry|Tags: 3:07, Chemistry, GCSE, GCSE_Chemistry_SpecPoint, SpecPoint, Topic: Energetics, Topic: Key Calculations, Triple|

(Triple only) Bond energy calculations – videos

Here are a couple of videos explaining how to do bond energy calculations:

Hydr0Gen2019-02-10T16:05:23+00:00Categories: Uncategorized|Tags: Chemistry, GCSE, Topic: Energetics, Topic: Key Calculations, Video|