Triple-Science-only spec point
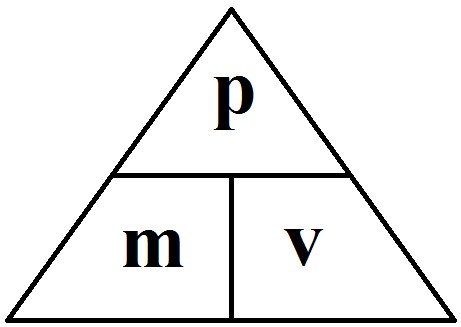
1.25 know and use the relationship between momentum, mass and velocity: P=m x v
momentum (kgm/s)= mass (kg) x velocity (m/s)
Triple-Science-only spec point
momentum (kgm/s)= mass (kg) x velocity (m/s)

To reduce the force experienced by the passenger you need to extend the time for a passenger to stop in a collision. As force is the change in momentum divided by time.

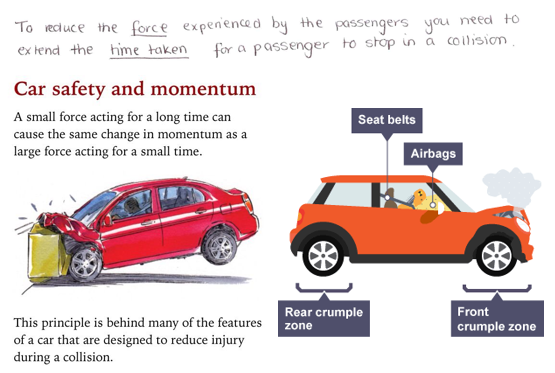
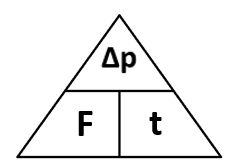
Force is the rate of change of momentum. So Force (N) = change in momentum (kgm/s) / time (s)
Every action has an equal and opposite reaction.
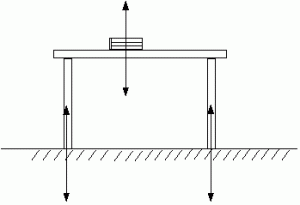
Book pushes down on table, table pushes up on book. So book doesn’t accelerate.
Table pushes down on floor, floor pushes up on table. So table doesn’t accelerate.
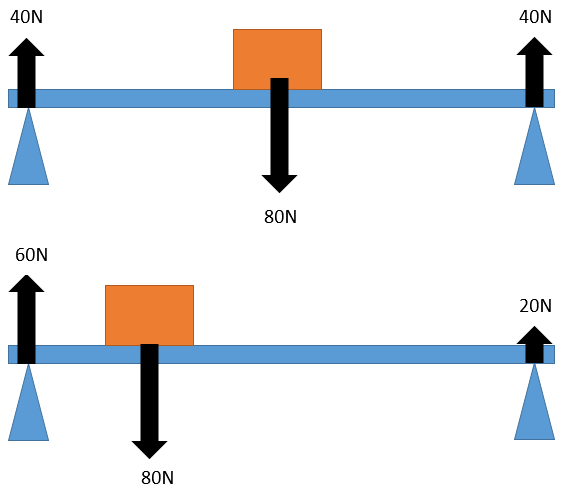
moment = force x perpendicular distance from the pivot
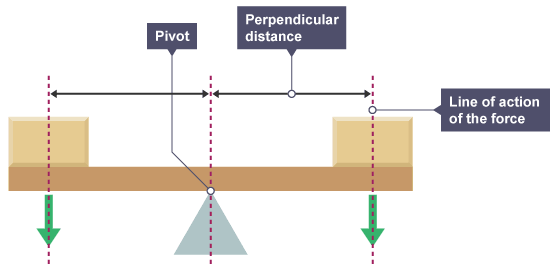
The principle of moments states that when the clockwise moments are equal to the anticlockwise moments a body will be in equilibrium.
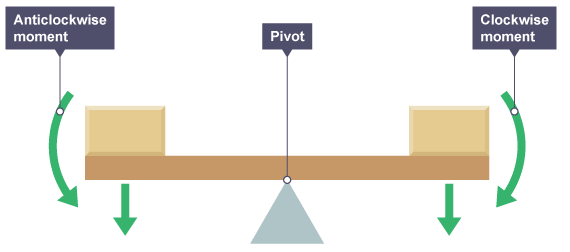
when moments are taken from the right hand side as the block is a greater distance the force from the left hand pivot must be bigger to counteract it. The opposite is true for the left hand side.
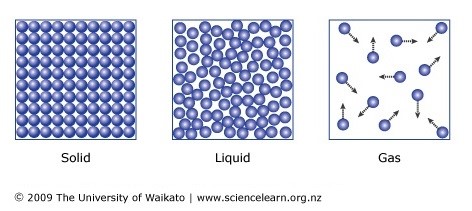
solids:
liquids:
gasses:
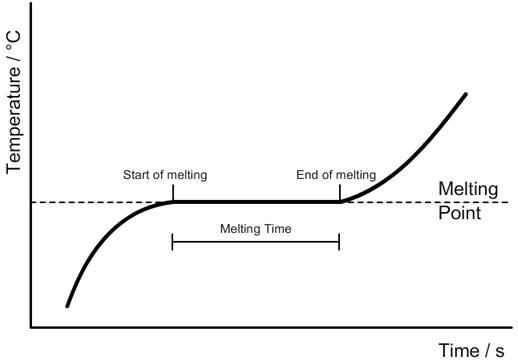
Specific heat capacity:
Change in thermal energy [J] = Mass [kg] x Specific heat capacity [J/kg 0C] x Change in temperature [0C]
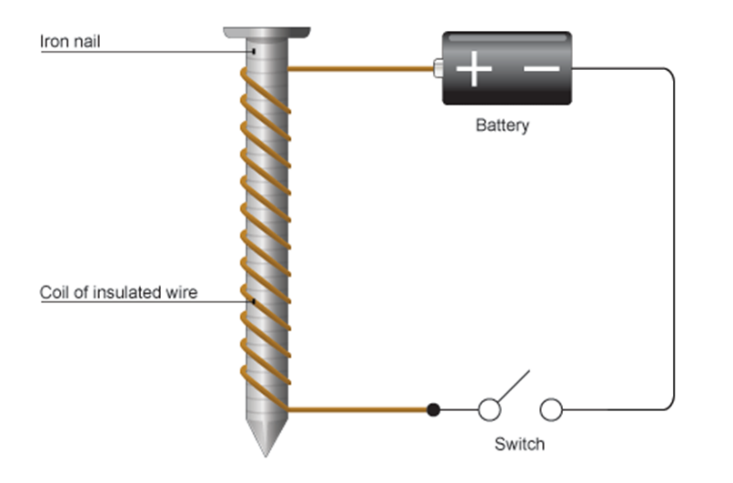
A soft iron core wrapped in wire. When current flows through the coil of wire it becomes magnetic.
|
The movement of the charged particle is a current so it produces a magnetic field. This magnetic field interacts with the permanent magnetic field to create a force. The force is perpendicular to the direction of motion and the permanent magnetic field. |
|
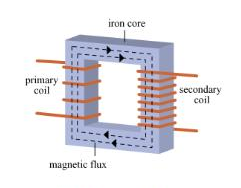
AC current in the primary coil produces a changing magnetic field around the primary coil. The iron core channels the changing field through the secondary coil. The changing magnetic field induces a voltage in the secondary coil. |
|
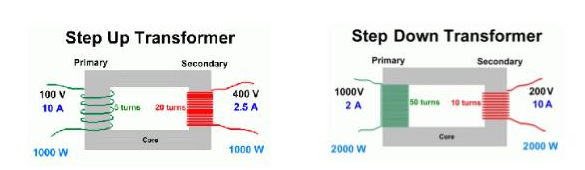
Step Up transformers increase the voltage – more secondary turns than primary Step Down transformers decrease the voltage – more primary turns than secondary |
Solubility is defined in terms of the maximum mass of a solute that dissolves in 100g of solvent. The mass depends on the temperature.
For example, the solubility of sodium chloride (NaCl) in water at 25⁰C is about 36g per 100g of water.
The solubility of solids changes as temperature changes. This can be plotted on a solubility curve.
The salts shown on this graph are typical: the solubility increases as temperature increases.
For example, the graph above shows that in 100g of water at 50⁰C the maximum mass of potassium nitrate (KNO₃) which will dissolve is 80g.
However, if the temperature were 80⁰C a mass of 160g of potassium nitrate (KNO₃) would dissolve in 100g of water.
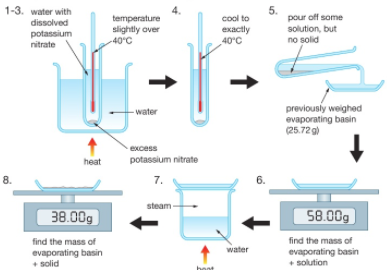
At a chosen temperature (e.g. 40⁰C) a saturated solution is created of potassium nitrate (KNO₃) for example.
Some of this solution (not any residual solid) is poured off and weighed. The water is then evaporated from this solution to leave a residue of potassium nitrate which is then weighed.
The difference between the two measured masses is the mass of evaporated water.
The solubility, in grams per 100g of water, is equal to 100 times the mass of potassium nitrate residue divided by the mass of evaporated water.
Concentration is a measurement of the amount of substance per unit volume.
In Chemistry, concentration is measured in mol/dm3 (read as moles per cubic decimetre).
The following formula allows for the interconversion between a concentration (in mol/dm3), the amount (in moles) of a substance in a solution, and the volume of the solution (in dm3).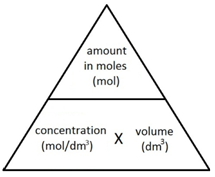
or
Note: 1 dm3 = 1000 cm3
For example, to convert 250 cm3 into dm3:
Example 1: 0.03 mol of sodium carbonate (Na2CO3) is dissolved in 300 cm3 of water. Calculate the concentration of the solution.
Step 1: Convert the volume of water from cm3 into dm3.
Step 2: Use the molar concentration formula to calculate of the concentration of the solution.
Example 2: Calculate the amount, in moles, of 25cm3 of hydrochloric acid (HCl) with a concentration of 2 mol/dm3.
Step 1: Convert the volume of HCl from cm3 into dm3.
Step 2: Rearrange the molar concentration formula to calculate of the amount, in moles of HCl.
Titration calculations, example 1
The titration method that is used to prepare a soluble salt is also used to determine the concentration of an unknown solution.
For example, a titration problem will look like this:
A pupil carried out a titration to find the concentration of a solution of hydrochloric acid (HCl). She found that 25.0 cm3 of 0.100 mol/dm3 sodium hydroxide solution (NaOH) required 23.50 cm3 of dilute hydrochloric acid for neutralisation. Calculate the concentration, in mol/dm3 of the acid.
The chemical equation for this reaction is:
NaOH(aq) + HCl(aq) –> NaCl(aq) + H2O(l)
volume 25.0cm3 23.50cm3
concentration 0.100mol/dm3
It can be useful, as shown above, to write the values of the volumes & concentration underneath the equation.
Step 1: Calculate the amount, in moles, of the solution that you know the values for both volume and concentration. In this case sodium hydroxide (NaOH).
First convert the volume of NaOH from cm3 into dm3.
Then rearrange the molar concentration formula to calculate of the amount, in moles of NaOH.
Step 2: Deduce the amount, in moles of the solution with the unknown concentration. In this case hydrochloric acid (HCl).
From the chemical equation the ratio of NaOH to HCl is 1:1
Therefore if you have 0.0025 mol of NaOH, this will react with 0.0025 mol of HCl.
Step 3: Calculate the concentration of the hydrochloric acid (HCl).
Convert the volume of HCl from cm3 into dm3.
Use the molar concentration formula to calculate of the concentration of the HCl.
Titration calculations, example 2
25.0 cm3 of sodium carbonate solution (Na2CO3) of unknown concentration was neutralised by 30.0 cm3 of 0.100 mol/dm3 nitric acid (HNO3).
Na2CO3(aq) + 2HNO3(aq) –> 2NaNO3(aq) + CO2(g) + H2O(l)
Calculate the concentration, in mol/dm3 of the sodium carbonate solution.
Step 1: Calculate the amount, in moles, of nitric acid (HNO3).
Step 2: Deduce the amount, in moles of sodium carbonate (Na2CO3).
Using the equation:
Na2CO3(aq) + 2HNO3(aq) –> 2NaNO3(aq) + CO2(g) + H2O(l)
Ratio Na2CO3:HNO3 = 1:2
Step 3: Calculate the concentration of sodium carbonate (Na2CO3).
Converting mol/dm3 into g/dm3
Concentration can also be expressed in g/dm3 (grams per cubic decimetre).
Therefore mol/dm3 can be converted into g/dm3.
Example: Convert 0.06 mol/dm3 of sodium carbonate (Na2CO3) into g/dm3
Step 1: calculate the relative formula mass (Mr) of sodium carbonate (Na2CO3).
Step 2: Recall the formula giving the relationship between mass, amount and formula mass.
therefore
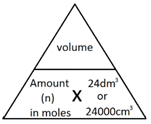
The molar volume of a gas is the volume that one mole of any gas will occupy.
1 mole of gas, at room temperature and pressure (rtp), will always occupy 24 dm3 or 24,000 cm3.
Note: 1 dm3 = 1000 cm3
The following formulae allows for the interconversion between a volume in dm3 or cm3 and a number of moles for a given gas:
or
Example 1:
Calculate the amount, in moles, of 12 dm3 of carbon dioxide (CO2).
Example 2:
Calculate the volume at rtp in cubic centimetres (cm3), of 3 mol of oxygen, (O2).
When metal atoms join together the outer electrons become ‘delocalised’ which means they are free to move throughout the whole structure.
Metals have a giant regular arrangement of layers of positive ions surrounded by a sea of delocalised electrons.
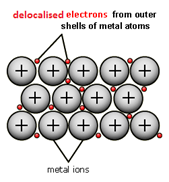
Metallic bonding is the strong electrostatic attraction between positive metal ions and a sea of delocalised electrons.

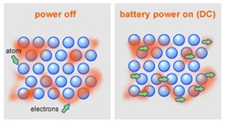
Metals are good conductors because they have delocalised electrons which are free to move.
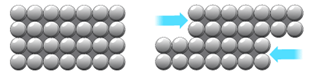
Metals are malleable (can be hammered into shape) because they have layers of ions that can slide over each other.
Electrical conductivity is the movement of charged particles.
In this case, charged particles means either delocalised electrons or ions.
These particles need to be free to move in a substance for that substance to be conductive.
Covalent compounds do not conduct electricity because there are no charged particles that are free to move.
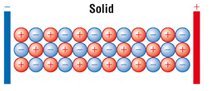
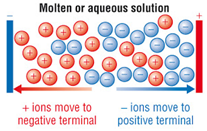
Ionic compounds only conduct electricity only when molten or in solution.
When solid the ions are not free to move.
When molten or in solution the ions are free to move.
A negative ion is called an anion. Examples are the bromide ion (Br⁻) and the oxide ion (O²⁻).
A positive ion is called a cation. Examples are the sodium ion (Na⁺) and the aluminium ion (Al³⁺).
A trick to remember this is to write the ‘t’ as a ‘+’ in the word cation: ca+ion
Electrolysis: The breaking down of a substance caused by passing an electric current through an ionic compound which is molten or in solution. New substances are formed.
ELECTROLYSIS OF MOLTEN IONIC COMPOUNDS
Example: The electrolysis of molten lead bromide (PbBr2)
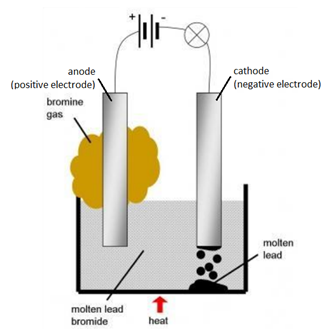
Solid lead bromide is heated and becomes molten. Explanation: ions become free to move.
Overall Reaction
word equation: lead bromide –> lead + bromine
chemical equation: PbBr2(l) –> Pb(l) + Br2(g)
Remember
OILRIG : Oxidation Is the Loss of electrons and Reduction Is the Gain of electrons
PANCAKE : Positive Anode, Negative Cathode
ELECTROLYSIS OF IONIC SOLUTIONS
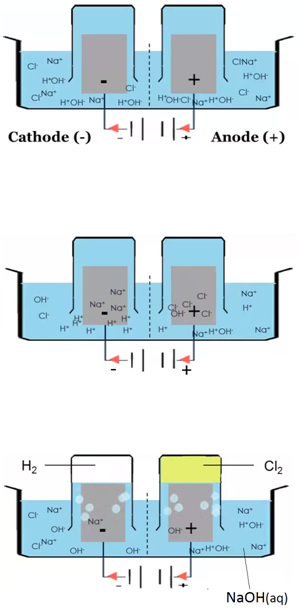
Rules for working out elements formed from electrolysis of solutions
Follow these rules to decide which ions in solution will react at the electrodes:
At the cathode
Metal ions and hydrogen ions are positively charged. Whether you get the metal or hydrogen during electrolysis depends on the position of the metal in the reactivity series:
At the anode
At the anode, the product of electrolysis is always oxygen gas (O2) unless the solution contains a high concentration of Cl–, Br- or I– ions, in which case a halogen is produced, e.g. chlorine gas (Cl2), bromine gas (Br2), and iodine gas (I2).
The electrolysis of sodium chloride solution (NaCl(aq))
Solid sodium chloride is dissolved in water. Explanation: The sodium ions and chloride ions become free to move.
H2O(l) ⇋ H+(aq) + OH–(aq)
Electron half equation: 2Cl–(aq) –> Cl2 (g) + 2e–
Electron half equation: 2H+(aq) + 2e– –> H2 (g)
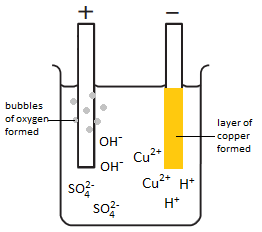
The electrolysis of copper sulfate solution (CuSO4(aq))
Electron half-equation: Cu2+(aq) + 2e– –> Cu (s)
Electron half-equation: 4OH–(aq) –> O2 (g) + 2H2O(l) + 4e–
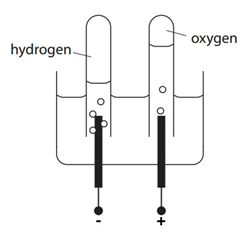
The electrolysis of sulfuric acid (H2SO4(aq))
Electron half-equation: 2H+(aq) + 2e– –> H2(g)
Electron half-equation: 4OH–(aq) –> O2 (g) + 2H2O(l) + 4e–
2H2O(l) –> 2H2(g) + O2(g)
There are twice the amount (in moles) of H2 compared to O2
Oxidation: the loss of electrons or the gain of oxygen
Reduction: the gain of electrons or the loss of oxygen
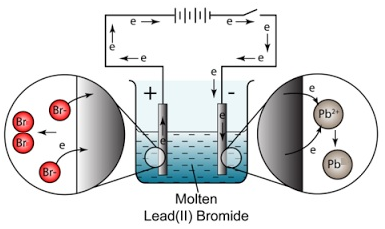
Example: The electrolysis of lead (II) bromide, PbBr2
At the cathode (negative electrode): Pb2+ (l) + 2e– → Pb (l) (reduction)
At the anode (positive electrode): 2Br– (l) → Br2 (g) + 2e– (oxidation)
Example: The electrolysis of aluminium oxide, Al2O3
At the cathode: Al3+ + 3e– → Al (reduction)
At the anode: 2O2- → O2 + 4e– (oxidation)
Example: The electrolysis of sodium chloride solution (NaCl (aq))
At the cathode: 2H+ (aq) + 2e– → H2 (g) (reduction)
At the anode: 2Cl– (aq) → Cl2 (g) + 2e– (oxidation)
Example: The electrolysis of copper sulfate solution (CuSO4 (aq))
At the cathode: Cu2+ (aq) + 2e– → Cu (s) (reduction)
At the anode: 4OH– (aq) → O2 (g) + 2H2O (l) + 4e– (oxidation)
The diagram shows an electrolytic cell.
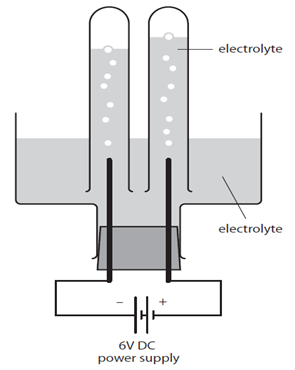
The electrolyte is an aqueous solution. For example it might be concentrated sodium chloride, NaCl (aq).
The test tubes over the electrodes must not completely cover them to make sure the ions are free to move throughout the solution.
In the case of NaCl (aq) bubbles of gas will be seen forming at the electrodes. These float up and collect in the test tubes when each gas can be tested to assess its identity.
As you go down the group the outer electron lost from the group 1 metal is further from the nucleus therefore the electron is less attracted by the nucleus and therefore more easily lost.
The higher up we go in group 7 (halogens) of the periodic table, the more reactive the element. The explanation concerns how readily these elements form ions, by attracting a passing electron to fill the outer shell.
In fluorine the outer electron shell is very close to the positively charged nucleus, so the attraction between this nucleus and the negatively charged electrons is very strong. This means fluorine is very reactive indeed.
However, for iodine the outer electron shell is much further from the nucleus so the attraction is weaker. This means iodine is less reactive.
Most metals are found in the Earth’s crust combined with other elements. Such compounds are found in rocks called ore, rocks from which it is worthwhile to extract a metal.
A few very unreactive metals, such as gold, are found native which means they are found in the Earth’s crust as the uncombined element.
Extraction of a metal from its ore typically involves removing oxygen from metal oxides.
If the ore contains a metal which is below carbon in the reactivity series then the metal is extracted by reaction with carbon in a displacement reaction.
If the ore contains a metal which is above carbon in the reactivity series then electrolysis (or reaction with a more reactive metal) is used to extract the metal.
Extraction of a metal from its ore typically involves removing oxygen from metal oxides.
If the ore contains a metal which is below carbon in the reactivity series then the metal is extracted by reaction with carbon in a displacement reaction.
If the ore contains a metal which is above carbon in the reactivity series then electrolysis (or reaction with a more reactive metal) is used to extract the metal.
| Aluminium | |
|---|---|
| Use | Property |
| Aircrafts and cans | Low density / resists corrosion |
| Power cables | Conducts electricity / ductile |
| Pots and pans | Low density / strong (when alloyed) / good conductor of electricity and heat |
Aluminium resists corrosion because it has a very thin, but very strong, layer of aluminium oxide on the surface.
| Copper | |
|---|---|
| Use | Property |
| Electrical wires | very good conductor of electricity and ductile |
| Pots and pans | very good conductor of heat / very unreactive / malleable |
| Water pipes | unreactive / malleable |
| Surfaces in hospitals | antimicrobial properties / malleable |
| Iron | |
|---|---|
| Use | Property |
| Buildings | Strong |
| Saucepans | Conducts heat / high melting point / malleable |
| Steel | ||
|---|---|---|
| Type of steel | Iron mixed with | Some uses |
| Mild steel | up to 0.25% carbon | nails, car bodies, ship building, girders |
| High-carbon steel | 0.6%-1.2% carbon | cutting tools, masonry nails |
| Stainless steel | Chromium (and nickel) | cutlery, cooking utensils, kitchen sinks |
Mild steel is a strong material that can easily be hammered into various shapes (malleable). It rusts easily.
High-carbon steel is harder than mild steel but more brittle (not as malleable).
Stainless steel forms a strong, protective oxide layer so is very resistant to corrosion.
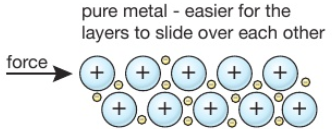
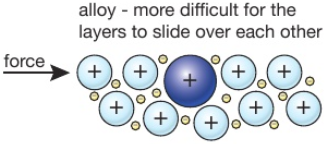
An alloy is a mixture of a metal with, usually, other metals or carbon.
For example, brass is a alloy of copper and zinc, and steel is an alloy of iron and carbon.
Alloys are harder than the individual pure metals from which they are made.
In an alloy, the different elements have slightly different sized atoms. This breaks up the regular lattice arrangement and makes it more difficult for layers of ions to slide over each other.
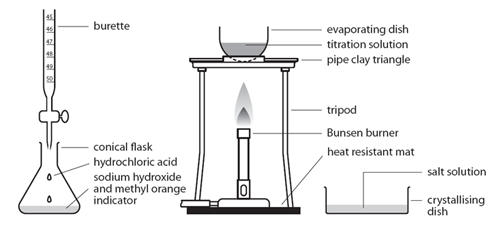
Titration is used to find out precisely how much acid neutralises a certain volume of alkali (or vice versa).
The diagram shows the titration method for a neutralisation reaction between hydrochloric acid and sodium hydroxide, using phenolphthalein as an indicator. The indicator changes colour when neutralisation occurs.
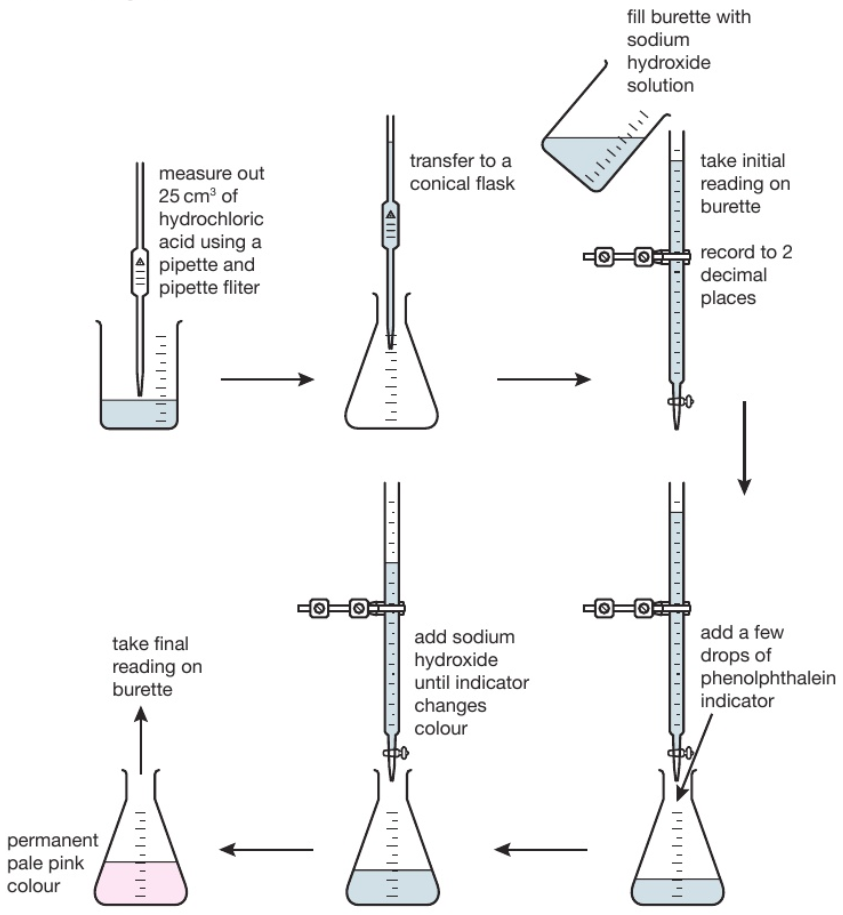
The conical flask is swirled to mix the solutions each time alkali is added. When reading the burette it is important to be aware that the numbers on the scale increase from top to bottom. Readings are usually recorded to the nearest 0.05cm³ so all readings should be written down with 2 decimal places. The second decimal place is given as a ‘0’ if the level of the solution is on a line, or ‘5’ if it is between the lines. The volume of alkali added is calculated by subtracting the final reading from the initial reading. Various indicators can be used such as phenolphthalein or methyl orange. However universal indicator should not be used since it has a wide range of colours rather than one specific colour change so it would be unclear when the precise endpoint of titration was achieved.
This process is repeated a number of times. The first time it is done roughly to get a good approximation of how much alkali needs to be added. On subsequent attempts, the alkali is added very slowly when approaching the correct volume.
Titration Method:
Preparing pure dry crystals of sodium chloride (NaCl) from hydrochloric acid (HCl) and sodium hydroxide (NaOH)
Before the salt preparation is carried out using the below method, the volume of acid that exactly reacts with 25cm3 of the alkali is found by titration using methyl orange indicator.
| Step | Explanation |
|---|---|
| Pipette 25cm3 of alkali (NaOH) into a conical flask | Accurately measures the alkali (NaOH) |
| Do not add indicator | Prevents contamination of the pure crystals with indicator |
| Using the titration values, titrate the known volume acid (HCl) into conical flask containing alkali | Exactly neutralises all of the alkali (NaOH) |
| Transfer to an evaporating basin & heat the solution | Forms a hot saturated solution (NaCl(aq)) |
| Allow the solution to cool so that hydrated crystals form | Sodium chloride is less soluble in cold water |
| Remove the crystals by filtration and wash with distilled water | Removes any impurities |
| Dry by leaving in a warm place | Evaporates the water |
(Note – This process could be reversed with the acid in the pipette and the alkali in the burette)
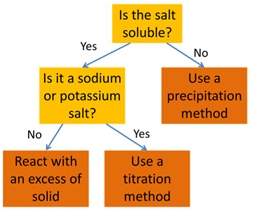
How to select the right method for preparing a salt:
Precipitation Method:
Preparing pure dry crystals of silver chloride (AgCl) from silver nitrate solution (AgNO3) and potassium chloride solution (KCl)
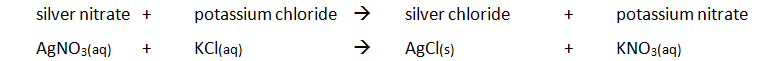
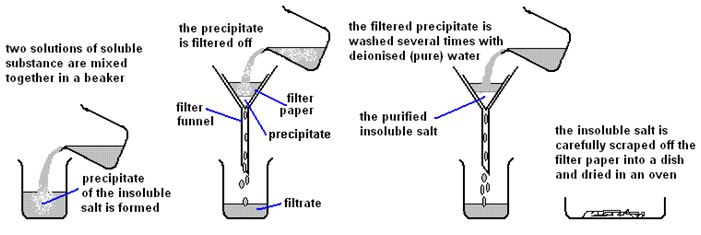
| Step | Explanation |
|---|---|
| Mix the two salt solutions together in a beaker | Forms a precipitate of an insoluble salt (AgCl) |
| Stir with glass rod | Make sure all reactants have reacted |
| Filter using filter paper and funnel | Collect the precipitate (AgCl) |
| Wash with distilled water | Removes any the other soluble salts (KNO3) |
| Dry by leaving in a warm place | Evaporates the water |
Objective: prepare a pure, dry sample of lead (II) sulfate (PbSO₄).
Preparing a pure, dry sample of lead (II) sulfate (PbSO₄) from lead (II) nitrate solution (Pb(NO₃)₂) and sodium sulfate solution (Na₂SO₄).
Pb(NO₃)₂ (aq) + Na₂SO₄ (aq) → PbSO₄ (s) + 2NaNO₃ (aq)
The symbol ΔH is used to represent the change in heat (or enthalpy change) of a reaction.
ΔH is measured in kJ/mol (kilojoules per mole).
The change in heat (enthalpy change) can be represented on an energy level diagram. ΔH must also labelled.
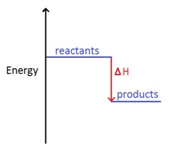
In an exothermic reaction, the reactants have more energy than the products.
Energy is given out in the form of heat which warms the surroundings.
ΔH is given a negative sign, because the reactants are losing energy as heat, e.g ΔH = -211 kJ/mol.
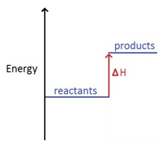
In an endothermic reaction, the reactants have less energy than the products.
Energy is taken in which cools the surroundings.
ΔH is given a positive sign, because the reactants are gaining energy, e.g ΔH = +211 kJ/mol.